题目内容
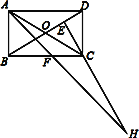
【题目】如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.
(1)求∠EDG的度数.
(2)如图2,E为BC的中点,连接BF.
①求证:BF∥DE;
②若正方形边长为12,求线段AG的长.


【答案】(1)45°;(2)①用外角证明平行见解析,②4
【解析】整体分析:
(1)判断DE,DG分别平分∠CDF,∠ADF;(2)①由ED平分∠CEG,EF=EB,结合三角形的一个外角等于和它不相邻的两个内角的和得到∠CED=∠EBF;(3)由(1)中的结论,在Rt△BEG中用勾股定理列方程求解.
(1)解:由折叠知,DF=DC,∠CDE=∠FDE,∠DFE=∠DCE=90°,
∵AD=CD,所以AD=DF,
∵∠DAG=90°,DG=DG,
∴△DAG≌△DFG,∴∠ADG=∠FDG,
∴∠EDG=∠EDF+∠FDG=![]() (∠CDF+∠FDA)=
(∠CDF+∠FDA)=![]() ×90°=45°.
×90°=45°.
(2)①证明:由折叠知,CE=EF,∠CED=∠FED,
∵E为BC的中点,∴BE=CE,∴EF=BE,
∴∠EBF=∠EFB,
∵∠CEG=∠EBF+∠EFB,∴∠CED=∠EBF,
∴BF∥DE.
(3)由(1)得EC=EF,GA=GF,
∴EG=EC+GA.
设AG=x,则BG=12-x,
又EB=EC=EF=6,
在Rt△BEG中,由勾股定理得:BG2+BE2=EG2.
∴(12-x)2+62=(x+6)2,解得x=4.
所以线段AG的长为4.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】随着人们的生活水平的提高,家用轿车越来越多地进入家庭.小明家买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣9 | ﹣13 | 0 | ﹣14 | ﹣16 | +33 | +19 |
(1)求出这7天的行驶路程中最多的一天比最少的一天多行驶多少千米?
(2)若每行驶100km需用汽油8升,每升汽油6.5元,计算小明家这7天的汽油费用共是多少元?