Question

【题目】如图，以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D，过D作半圆的切线与边AC交于点E，过E作EF∥AB，与BC交于点F．若AB=20，OF=7.5，则CD的长为（　　）

A.7
B.8
C.9
D.10

Answer 1

【答案】C
【解析】解：连结AD，如图，
∵AB为直径，
∴∠ADB=90°，
∴∠1+∠ADE=90°，∠2+∠C=90°，
∵DE为切线，
∴ED=EA，
∴∠ADE=∠2，
∴∠1=∠C，
∴ED=EC，
∴CE=AE，
∵EF∥AB，
∴EF为△ABC的中位线，
∴BF=CF，
而BO=AO，
∴OF为△ABC的中位线，
∴OF∥AE，
∴AE=OF=7.5，
∴AC=2AE=15，
在Rt△ACD中，BC===25，
∵∠DCA=∠ACB，
∴△CDA∽△CAB，
∴= ， 即= ，
∴CD=9．
故选C．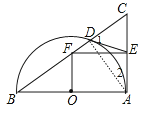

【考点精析】利用切线的性质定理对题目进行判断即可得到答案，需要熟知切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．