题目内容
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
A.4
B.6
C.3![]()
D.2![]()
【答案】B
【解析】解:连接OD,
∵DF为圆O的切线,
∴OD⊥DF,
∵△ABC为等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵OD=OC,
∴△OCD为等边三角形,
∴∠CDO=∠A=60°,∠ABC=∠DOC=60°,
∴OD∥AB,
∴DF⊥AB,
在Rt△AFD中,∠ADF=30°,AF=2,
∴AD=4,即AC=8,
∴FB=AB﹣AF=8﹣2=6,
在Rt△BFG中,∠BFG=30°,
∴BG=3,
则根据勾股定理得:FG=3![]() .
.
故选:B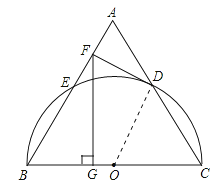
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目
【题目】列方程组解应用题:
为了保护环境,深圳某公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如下表:
A | B | |
价格(万元/台) | a | b |
节省的油量(万升/年) | 2.4 | 2 |
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.
(1)请求出a和b;
(2)若购买这批混合动力公交车每年能节省22.4万汽油,求购买这批混合动力公交车需要多少万元?