题目内容
【题目】如图，PA、PB是⊙O的切线，CD切⊙O于点E，△PCD的周长为12，∠APB=60°．求：
（1）PA的长；
（2）∠COD的度数．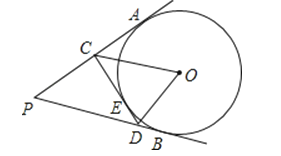
【答案】解：（1）∵CA，CE都是圆O的切线，
∴CA=CE，
同理DE=DB，PA=PB，
∴三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12，
即PA的长为6；
（2）∵∠P=60°，
∴∠PCE+∠PDE=120°，
∴∠ACD+∠CDB=360°﹣120°=240°，
∵CA，CE是圆O的切线，
∴∠OCE=∠OCA=
∠ACD；
同理：∠ODE=∠CDB，
∴∠OCE+∠ODE=（∠ACD+∠CDB）=120°，
∴∠COD=180﹣120°=60°．
【解析】（1）可通过切线长定理将相等的线段进行转换，得出三角形PDE的周长等于PA+PB的结论，即可求出PA的长；
（2）根据三角形的内角和求出∠ADC和∠BEC的度数和，然后根据切线长定理，得出∠EDO和∠DEO的度数和，再根据三角形的内角和求出∠DOE的度数．
【考点精析】掌握切线的性质定理是解答本题的根本，需要知道切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．
练习册系列答案
相关题目
【题目】列方程组解应用题：
为了保护环境，深圳某公交公司决定购买一批共10台全新的混合动力公交车，现有A、B两种型号，其中每台的价格，年省油量如下表：
A | B | |
价格（万元/台） | a | b |
节省的油量（万升/年） | 2.4 | 2 |
经调查，购买一台A型车比购买一台B型车多20万元，购买2台A型车比购买3台B型车少60万元．
（1）请求出a和b；
（2）若购买这批混合动力公交车每年能节省22.4万汽油，求购买这批混合动力公交车需要多少万元？
