Question

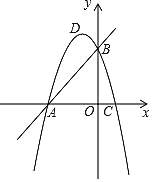
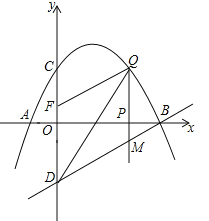
【题目】如图，已知抛物线经过点A（-1,0），B（4,0）C（0,2）三点，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P做x轴的垂线交抛物线于点Q，交直线BD于点M．

（1）求该抛物线所表示的二次函数的表达式；

（2）已知点F（0，），当点P在x轴上运动时，试求m为何值时，四边形DMQF是平行四边形？

Answer 1

【答案】（1）y=﹣x2+x+2；（2）m=﹣1或m=3时，四边形DMQF是平行四边形．

【解析】

（1）待定系数法求解可得；

（2）先利用待定系数法求出直线BD解析式为y=x﹣2，则Q（m，﹣m2+m+2）、M（m，m﹣2），由QM∥DF且四边形DMQF是平行四边形知QM=DF，据此列出关于m的方程，解之可得．

（1）由抛物线过点A（﹣1，0）、B（4，0）可设解析式为y=a（x+1）（x﹣4），将点C（0，2）代入，得：﹣4a=2，解得：a=﹣，则抛物线解析式为y=﹣（x+1）（x﹣4）=﹣x2+x+2；

（2）由题意知点D坐标为（0，﹣2），设直线BD解析式为y=kx+b，将B（4，0）、D（0，﹣2）代入，得：，解得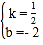：，∴直线BD解析式为y=x﹣2．

∵QM⊥x轴，P（m，0），∴Q（m，﹣m2+m+2）、M（m，m﹣2），则QM=﹣m2+m+2﹣（m﹣2）=﹣m2+m+4．

∵F（0，）、D（0，﹣2），∴DF=．

∵QM∥DF，∴当﹣m2+m+4=时，四边形DMQF是平行四边形，解得：m=﹣1或m=3，即m=﹣1或m=3时，四边形DMQF是平行四边形．