题目内容
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.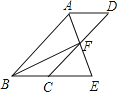
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,∴BE=CD
(2)
解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF= ![]() =
= ![]() =2
=2 ![]() ,
,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
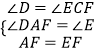 ,
,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积= ![]() AEBF=
AEBF= ![]() ×4×2
×4×2 ![]() =4
=4 ![]() .
.
【解析】(1)由平行四边形的性质和角平分线得出∠BAE=∠BEA,即可得出AB=BE;
(2)先证明△ABE是等边三角形,得出AE=AB=4,AF=EF=2,由勾股定理求出BF,由AAS证明△ADF≌△ECF,得出△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积= ![]() AEBF,即可得出结果.此题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定、等边三角形的判定与性质、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题(2)的关键.
AEBF,即可得出结果.此题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定、等边三角形的判定与性质、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题(2)的关键.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?