题目内容
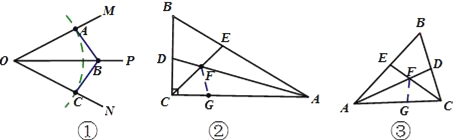
【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.

【答案】(1)画图见解析;(2)DF=EF,理由见解析;(3)DF=EF 仍然成立,理由见解析.
【解析】(1)在∠MON的两边上以O为端点截取相等的两条相等的线段,两个端点与角平分线上任意一点相连,所构成的两个三角形全等,即△COB≌△AOB;
(2)根据图(1)的作法,在CG上截取CG=CD,证得△CFG≌△CFD(SAS),得出DF=GF;再根据ASA证明△AFG≌△AFE,得EF=FG,故得出EF=FD;
(3)根据图(1)的作法,在CG上截取AG=AE,证得△EAF≌△GAF(SAS),得出FE=FG;再根据ASA证明△FDC≌△FGC,得DF=FG,故得出EF=FD.
解:(1)如图①所示,△COB≌△AOB,点C即为所求.
(2)如图②,在CG上截取CG=CD,
∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD中,
CG=CD,∠DCF=∠GCF,CF=CF,
∴△CFG≌△CFD(SAS),
∴DF=GF.
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠ACB,且∠EAF=∠GAF,
∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA=![]() (∠BAC+∠ACB)=
(∠BAC+∠ACB)=![]() =60°,
=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,
∠AFE=∠AFG,AF=AF,∠EAF=∠GAF,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴DF=EF;
(3)DF=EF 仍然成立.
证明:如图③,在CG上截取AG=AE,
同(2)可得△EAF≌△GAF(SAS),
∴FE=FG,∠EFA=∠GFA.
又由题可知,∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠ACB,
∠ACB,
∴∠FAC+∠FCA=![]() (∠BAC+∠ACB)=60°,
(∠BAC+∠ACB)=60°,
∴∠AFC=180°﹣(∠FAC+∠FCA)=120°,
∴∠EFA=∠GFA=180°﹣120°=60°=∠DFC,
∴∠CFG=∠CFD=60°,
同(2)可得△FDC≌△FGC(ASA),
∴FD=FG,
∴FE=FD.
“点睛”此题主要考查全等三角形的判定和性质的运用,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具,在判定三角形全等时,关键是选择恰当的判定条件,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造全等三角形.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案【题目】某中学为了解某年级1200名学生每学期参加社会实践活动时间,随机对该年级50名学生进行了调查,结果如下表:
时间(天) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
人 数 | 1 | 2 | 4 | 5 | 7 | 11 | 8 | 6 | 4 | 2 |
(1)在这个统计中,众数是 ,中位数是 ;
(2)补全下面的频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
3.5~5.5 | 3 | 0.06 |
5.5~7.5 | 9 | 0.18 |
7.5~9.5 | 0.36 | |
9.5~11.5 | 14 | |
11.5~13.5 | 6 | 0.12 |
合 计 | 50 | 1.00 |

(3)请你估算这所学校该年级的学生中,每学期参加社会实践活动时间不少于9天的大约有多少人?
【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 14 | 35 |
售价(元/件) | 20 | 43 |
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.