题目内容
【题目】已知一个零刻度落在点A的量角器(半圆O)的直径为AB,等腰直角△BCD绕点B旋转.
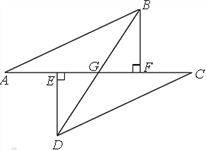
(1)如图1,当等腰直角△BCD运动至斜边BD交量角器边缘于点G,直角边CD交量角器边缘于点E,F,第三边交量角器边缘于点H时,点G在量角器上的读数为20°,求此时点H在量角器上的读数.
(2)如图2,当点G,E在量角器上的读数α,β满足什么关系时,等腰直角△BCD的直角边CD会与半圆O相切于点E?请说明理由.

【答案】(1)、110°;(2)、β=![]() α+45°
α+45°
【解析】
试题分析:(1)、连接OG、OH.由题意可知:∠AOG=20°,由等腰直角三角形的性质可求得∠CBD=45°,接下来,依据圆周角定理可求得∠HOG=90°,最后依据∠AOH=∠AOG+∠GOH求解即可;(2)、连接OG、OE.先由切线的性质证明OE⊥DC,然后依据平行线的判定定理可证明EO∥CB,接下来依据平行线的性质和可得到∠EOA=∠CBA,最后结合圆周角定理以及∠ABC、∠ABG、∠DBC的关系可得到α、β的关系.
试题解析:(1)、如图1所示:连接OG、OH.
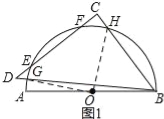
∵点G在量角器上的读数为20°, ∴∠AOG=20°. ∵△BCD为等腰直角三角形,
∴∠CBD=45°. ∴∠HOG=90°. ∴∠AOH=∠AOG+∠GOH=20°+90°=110°.
(2)、如图2所示:连接OG、OE.
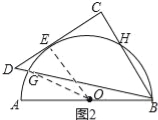
∵DC为圆O的切线,E为切点, ∴∠OED=90°. ∴∠OED=∠C. ∴EO∥CB.
∴∠EOA=∠CBA=β. 又∵∠GBA=![]() ∠GOA=
∠GOA=![]() α,∠ABC=∠ABG+∠DBC, ∴β=
α,∠ABC=∠ABG+∠DBC, ∴β=![]() α+45°.
α+45°.

练习册系列答案
相关题目