题目内容
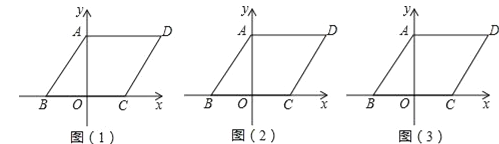
【题目】如图，∠ACB=90°，AC=BC，D为△ABC外一点，且AD=BD，DE⊥AC交CA的延长线于点E，
（1）求证：DE=AE+BC .
（2）若
，求线段AE的长.
【答案】（1）见详解；（2）1
【解析】
（1）连接CD，利用垂直平分线的判定即可得CD垂直平分AB，再利用三线合一得到∠ACD=
∠ACB，然后证出△ECD为等腰直角三角形得到DE=EC即可.
（2）先证△CAD≌△CBD，可得S △CAD= S△CBD=
，再利用三角形的面积和高求出底AC，再利用（1）的结论就可求出AE.
（1）连接CD
∵AC=BC，AD=BD
∴点C和点D都在AB垂直平分线上
∴CD垂直平分AB
∴CD平分∠ACB
∵∠ACB=90°
∴∠ACD=∠ACB=45°
∵DE⊥AC
∴△ECD为等腰直角三角形，DE=EC
∵EC=AE＋AC= AE＋BC
∴DE=AE+BC.
（2）在△CAD和△CBD中
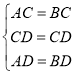
∴△CAD≌△CBD（SSS）
∴S△CAD= S△CBD=
∵DE=3
∴AC=2 S△CAD÷DE=2
∵DE= EC=AE+AC
∴AE= DE－AC=1
练习册系列答案
阅读快车系列答案
相关题目
