Question

【题目】已知一次函数的图象经过（2，5）和（﹣1，2）两点．

（1）求此一次函数的解析式；

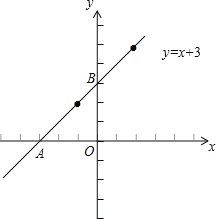
（2）用描点法在坐标系中画出这个函数的图象，求函数图象与x轴交点A、与y轴交点B的坐标；

（3）求△AOB的面积．

Answer 1

【答案】（1）y=x+3；（2）A（﹣3，0），点B（0，3）；（3）△AOB的面积是：．

【解析】

试题分析：（1）根据一次函数的图象经过（2，5）和（﹣1，2）两点，可以求得此一次函数的解析式；

（2）根据一次函数的图象经过（2，5）和（﹣1，2）两点，可以画出该函数的图象，然后将y=0代入（1）中求得的函数解析式，可以求得此时x的值，即可求得点A的坐标，再将x=0代入（1）中求得的函数解析式，可以求得此时y的值，即可求得点B的坐标；

（3）根据（2）中点A、B的坐标可以求得△AOB的面积．

解：（1）设过（2，5）和（﹣1，2）两点的函数解析式为y=kx+b，

则，

解得，，

即此一次函数的解析式为y=x+3；

（2）函数图象如右图所示，

将y=0代入y=x+3，得x=﹣3，

将x=0代入y=x+3，得y=3，

即点A（﹣3，0），点B（0，3）；

（3）∵点A（﹣3，0），点B（0，3），

∴OA=3，OB=3，

∴△AOB的面积是：．