题目内容
【题目】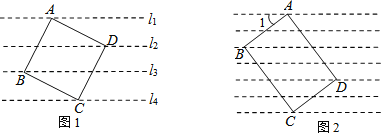
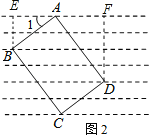
(1)如图1,4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线的距离都是2cm,正方形ABCD的4个顶点A、B、C、D分别在l1、l3、l4、l2上,求该正方形的面积;
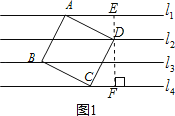
(2)如图2,把一张矩形卡片ABCD放在每格宽度为18mm的横格纸中,恰好四个顶点都在横格线上,已知∠1=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
【答案】(1)正方形ABCD的面积为20cm2;(2)矩形ABCD的周长=300mm.
【解析】
试题分析:(1)过D点作直线EF与平行线垂直,与l1交于点E,与l4交于点F.易证△ADE≌△DFC,得CF=2,DF=4.根据勾股定理可求CD2得正方形的面积;
(2)作BE⊥l于点E,DF⊥l于点F,求∠ADF的度数,在Rt△ABE中,可以求得AB的值,在Rt△ADF中,可以求得AD的值,即可计算矩形ABCD的周长,即可解题.
解:(1)如图1,作EF⊥l2,交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠AED=∠DFC=90°.
∵四边形ABCD为正方形,
∴∠ADC=90°.
∴∠ADE+∠CDF=90°.
又∵∠ADE+∠DAE=90°,
∴∠CDF=∠DAE.
∵AD=CD,
在△ADE和△DCF,
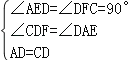 ,
,
∴△ADE≌△DCF(AAS),
∴CF=DE=2.
∵DF=4,
∴CD2=22+42=20,
即正方形ABCD的面积为20cm2;
(2)如图2,作BE⊥l于点E,DF⊥l于点F.
∵∠1+∠DAF=180°﹣∠BAD=180°﹣90°=90°,∠ADF+∠DAF=90°,
∴∠ADF=∠1=36°,
根据题意,得BE=36mm,DF=72mm.
在Rt△ABE中,sin∠1=![]() ,
,
∴AB=![]() =60mm,
=60mm,
在Rt△ADF中,cos∠ADF=![]() ,
,
∴AD=![]() mm=90mm.
mm=90mm.
∴矩形ABCD的周长=2(60+90)=300mm.

【题目】已知一次函数的图象经过(2,5)和(﹣1,2)两点.
(1)求此一次函数的解析式;
(2)用描点法在坐标系中画出这个函数的图象,求函数图象与x轴交点A、与y轴交点B的坐标;
(3)求△AOB的面积.
【题目】某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):
成绩(分) | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
人数(人) | 1 | 3 | 2 | 2 | 1 | 2 | 2 |
这13名学生听力测试成绩的中位数是( )
A. 16分 B. 17分 C. 18分 D. 19分