��Ŀ����
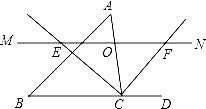
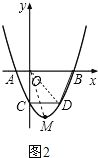
����Ŀ����ͼ1��������y=x2��2x+k��x�ύ��A��B���㣬��y�ύ�ڵ�C��0����3����[ͼ2��ͼ3Ϊ�����ͼ]
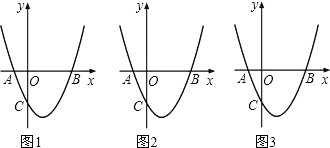
��1��k= ����A������Ϊ ����B������Ϊ ��
��2����������y=x2��2x+k�Ķ���ΪM�����ı���ABMC�������
��3����x���·������������Ƿ����һ��D��ʹ�ı���ABDC�������������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�
��4����������y=x2��2x+k�����Q��ʹ��BCQ����BCΪֱ�DZߵ�ֱ�������Σ�
���𰸡���1����3������1��0������3��0������2��9��
��3�����ڵ�D��![]() ��
��![]() ����ʹ�ı���ABDC��������Ϊ
����ʹ�ı���ABDC��������Ϊ![]() ��
��
��4�����������ϴ��ڵ�Q1����2��5����Q2��1����4����ʹ��BCQ1����BCQ2����BCΪֱ�DZߵ�ֱ�������Σ�
��������
�����������1����C��0����3�����������߽���ʽ�ɵ�kֵ����y=0���ɵ�A��B����ĺ����ꣻ
��2����M����x��Ĵ��ߣ����ı���ABMC�ָ������ֱ�������κ�һ��ֱ�����Σ������ǵ�����ͣ�
��3����D��m��m2��2m��3��������OD�����ı���ABDC������ֳ���AOC����DOC����DOB������ͣ������ʽ�����ֵ����4�������ֿ��ܣ�BΪֱ�Ƕ��㡢CΪֱ�Ƕ��㣬Ҫ�����ʶ��OBC�������ԣ��ǵ���ֱ�������Σ�����ͨ����ֱ���������������߶εij��ȣ�
�⣺��1����C��0����3�����������߽���ʽy=x2��2x+k�е�k=��3
��y=x2��2x��3��
��y=0��
��x2��2x��3=0��
���x1=��1��x2=3��
��A����1��0����B��3��0����
��2����y=x2��2x��3=��x��1��2��4��
�������ߵĶ���ΪM��1����4��������OM��
����AOC�����=![]() ����MOC�����=
����MOC�����=![]() ��
��
��MOB�����=6��
���ı���ABMC�����=��AOC�����+��MOC�����+��MOB�����=9��
˵����Ҳ�ɹ���M�������ߵĶԳ��ᣬ���ı���ABMC����
��ת��Ϊ��1��������2��ֱ������������ĺͣ�
��3����ͼ��2������D��m��m2��2m��3��������OD��
��0��m��3��m2��2m��3��0
����AOC�����=![]() ����DOC�����=
����DOC�����=![]() m��
m��
��DOB�����=��![]() ��m2��2m��3����
��m2��2m��3����
���ı���ABDC�����=��AOC�����+��DOC�����+��DOB�����
=��![]() m2+
m2+![]() m+6
m+6
=��![]() ��m��
��m��![]() ��2+
��2+![]() ��
��
�����ڵ�D��![]() ��
��![]() ����ʹ�ı���ABDC��������Ϊ
����ʹ�ı���ABDC��������Ϊ![]() ��
��
��4�������������
��ͼ��3��������B��BQ1��BC�����������ڵ�Q1����y���ڵ�E������Q1C��
�ߡ�CBO=45����
���EBO=45����BO=OE=3��
����E��������0��3����
��ֱ��BE�Ľ���ʽΪy=��x+3��
��![]()
���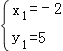
![]()
����Q1����������2��5����
��ͼ��4��������C��CF��CB�����������ڵ�Q2����x���ڵ�F������BQ2��
�ߡ�CBO=45����
���CFB=45����OF=OC=3��
����F����������3��0����
��ֱ��CF�Ľ���ʽΪy=��x��3��
��![]()
���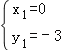
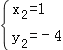
����Q2��������1����4����
���ϣ����������ϴ��ڵ�Q1����2��5����Q2��1����4����ʹ��BCQ1����BCQ2����BCΪֱ�DZߵ�ֱ�������Σ�
˵������ͼ��4������Q2�������߶���M��ֱ��֤����BCMΪֱ��������ͬ�����ԣ�



 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д� ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д�