题目内容
【题目】(旧知再现)圆内接四边形的对角 .
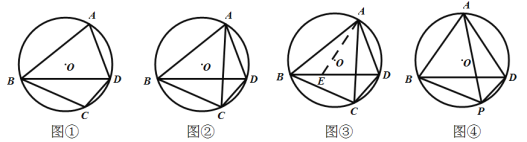
如图①,四边形![]() 是
是![]() 的内接四边形,若
的内接四边形,若![]() ,则
,则![]()
![]() .
.
(问题创新)圆内接四边形的边会有特殊性质吗?
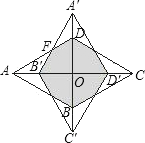
如图②,某数学兴趣小组进行深入研究发现:![]()
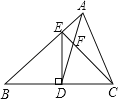
证明:如图③,作![]() ,交
,交![]() 于点
于点![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() 即
即![]() (请按他们的思路继续完成证明)
(请按他们的思路继续完成证明)
(应用迁移)如图④,已知等边![]() 外接圆
外接圆![]() ,点
,点![]() 为
为![]() 上一点,且
上一点,且![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】【旧知再现】互补, 110;【问题创新】见解析;【应用迁移】![]()
【解析】
【重温旧知】根据圆周角定理,得出![]() ,
,![]() ,化简得出
,化简得出![]() ,利用等腰三角形的两个底角相等和圆内接四边形对角互补,即可得
,利用等腰三角形的两个底角相等和圆内接四边形对角互补,即可得![]() ;
;
【提出问题】所得等式两边加上ADBC,右边变形后即可得证;
【应用迁移】由上题的结论,根据![]() 为等边三角形,可得AB=AC=BC,代入化简即可求出PA的长.
为等边三角形,可得AB=AC=BC,代入化简即可求出PA的长.
(1)如图示:
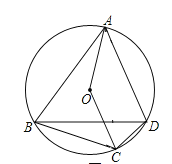
连接OA,OC,根据圆周角定理,
则有:![]() ,
,![]()
∴![]()
∴圆内接四边形的对角互补;
∵![]() ,
,
∴在等腰三角形ABD中,
![]()
∴![]()
(2)证明:如图,

∵![]()
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]()
∴![]() ,即
,即![]()
∴![]() ,
,
∴![]() ,
,
(3)

由(2)可知![]()
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() 即
即![]() .
.

练习册系列答案
相关题目