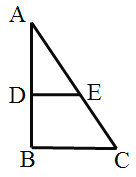题目内容
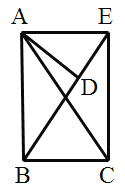
【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
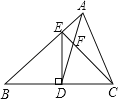
(1)求证:△ABC~△FCD;
(2)若△DEF的面积为2,求△FCD的面积.
【答案】(1)见解析;(2)6
【解析】
(1)由线段垂直平分线的性质可得BE=EC,进而可得∠ABC=∠FCD,由等腰三角形的性质可得∠ACB=∠FDC,问题即得解决;
(2)由相似三角形的性质可得AC=2DF,S△ABC=4S△FCD,进而可得AF=DF,S△DEC=S△AEC,再利用S△ABC与S△FCD的关系得出关于S△FCD的方程,即可求解.
解:(1)∵D是BC的中点,DE⊥BC,
∴BE=EC,BD=CD=![]() BC,
BC,
∴∠ABC=∠FCD,
∵AD=AC,
∴∠ACB=∠FDC,
∴△ABC∽△FCD;
(2)∵△ABC∽△FCD,
∴![]() ,∴
,∴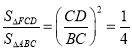 ,
,
∴AC=2DF,S△ABC=4S△FCD,
∴AD=2DF, ∴AF=DF,
∴S△DEF=S△AEF=2,S△DFC=S△AFC,
∴S△DEC=S△AEC,
∵BD=DC,
∴S△BDE=S△CDE=S△DFC+2,
∵S△ABC=4S△FCD,
∴3(S△DFC+2)=4S△FCD,
∴S△FCD=6.

练习册系列答案
相关题目