题目内容
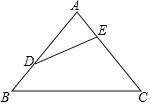
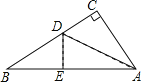
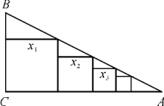
【题目】如图所示，在Rt△ABC中，∠C=90°，BC=1，AC=4，把边长分别为
，
，
，…，
的n
个正方形依次放入△ABC中，则第n个正方形的边长
_______________（用含n的式子表示）．
【答案】
【解析】
根据正方形的对边平行证明△BDF∽△BCA，然后利用相似三角形对应边成比例列出比例式即可求出第1个正方形的边长，同理利用前两个小正方形上方的三角形相似，根据相似三角形对应边成比例列出比例式即可求出前两个小正方形的边长的关系，以此类推，找出规律便可求出第n个正方形的边长．
解：如下图所示，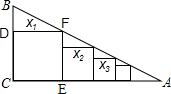
∵四边形DCEF是正方形，
∴DF∥CE，
∴△BDF∽△BCA，
∴DF：AC=BD：BC，
即x1：4=（1-x1）：1
解得x1= 
，
同理，前两个小正方形上方的三角形相似，
解得x2=x12
同理可得，
解得：
以此类推，第n个正方形的边长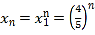
.
故答案为：
练习册系列答案
文敬图书课时先锋系列答案
相关题目
