题目内容
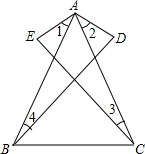 已知:如图,AC=AB,AE=AD,∠1=∠2.求证:∠3=∠4.
已知:如图,AC=AB,AE=AD,∠1=∠2.求证:∠3=∠4.分析:将∠3和∠4分别放在△AEC和△ADB中,只需证明两三角形全等可得出∠3=∠4,分析条件:AC=AB,AE=AD,差一个夹角,故由∠1=∠2,在等式两边都加上∠BAC,得到∠EAC=∠DAB,利用SAS可得出两三角形全等,利用全等三角形的对应角相等可得证.
解答:证明:∵∠1=∠2,
∴∠1+∠ABC=∠2+∠BAC,即∠EAC=∠DAB,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(SAS),
∴∠3=∠4.
∴∠1+∠ABC=∠2+∠BAC,即∠EAC=∠DAB,
在△AEC和△ADB中,
|
∴△AEC≌△ADB(SAS),
∴∠3=∠4.
点评:此题考查了全等三角形的判定与性质,利用了等式的性质,熟练掌握全等三角形的判定与性质是本题证明的关键.

练习册系列答案
相关题目
 29、已知:如图,AC=BD,DF=CE,∠ECB=∠FDA.求证:AF=BE.
29、已知:如图,AC=BD,DF=CE,∠ECB=∠FDA.求证:AF=BE. 16、已知:如图,AC=DF,AC∥FD,AE=DB,则根据
16、已知:如图,AC=DF,AC∥FD,AE=DB,则根据 是切点,
是切点, 12、已知:如图,AC、BD交于O点,OA=OC,OB=OD、则不正确的结果是( )
12、已知:如图,AC、BD交于O点,OA=OC,OB=OD、则不正确的结果是( ) 已知:如图,AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,在AB上有一点M,且CM=CD.
已知:如图,AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,在AB上有一点M,且CM=CD.