题目内容
【题目】如图所示，我国两艘海监船
，
在南海海域巡航，某一时刻，两船同时收到指令，立即前往救援遇险抛锚的渔船
.此时，船在船的正南方向5海里处，船测得渔船在其南偏东
方向，船测得渔船在其南偏东
方向.已知船的航速为30海里/小时，船的航速为25海里/小时，问船至少要等待多长时间才能得到救援？（参考数据：
，
，
，
）
【答案】C船至少要等待0.94小时才能得到救援.
【解析】
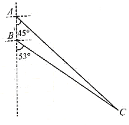
试题分析：过点C作
交AB的延长线于点D，可得∠CDA=90°，根据题意可知∠CDA=45°，设CD=x，则AD=CD=x，在Rt△BDC中，根据三角函数求得CD、BC的长，在Rt△ADC中，求得AC的长，再分别计算出B船到达C船处约需时间和A船到达C船处约需时间，比较即可求解.
试题解析：过点C作交AB的延长线于点D，则∠CDA=90°
已知∠CDA=45°，设CD=x，则AD=CD=x
∴BD=AD-AB=x-5
在Rt△BDC中，CD=BD·tan53°，即x=（x-5）·tan53°
∴
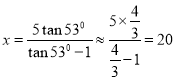
∴BC=
∴B船到达C船处约需时间：25÷25=1（小时）
在Rt△ADC中，AC=
1.41×20=28.2
∴A船到达C船处约需时间：28.2÷30=0.94（小时）
而0.94<1，所以C船至少要等待0.94小时才能得到救援.
练习册系列答案
相关题目
