题目内容
等腰三角形底边上的高等于底边的一半,则这个等腰三角形的顶角度数是
- A.30°
- B.45°
- C.90°
- D.120°
C
分析:作出图形,根据等腰三角形三线合一的性质可知底边上的高也是底边的中线,求出三角形被分成两个等腰直角三角形,求出两底角,再根据三角形的内角和定理即可求出顶角的度数.
解答: 解:如图,根据题意,AD=
解:如图,根据题意,AD= BC,
BC,
∵△ABC是等腰三角形,且AB=AC,AD⊥BC,
∴BD=CD,
∴△ABD,△ACD是等腰直角三角形,
∴∠B=∠C=45°,
∴∠BAC=180°-45°×2=90°,
即这个等腰三角形的顶角度数是90°.
故选C.
点评:本题考查了等腰三角形三线合一的性质,等腰三角形的两底角相等的性质,作出图形形象直观,更有助于问题的解决.
分析:作出图形,根据等腰三角形三线合一的性质可知底边上的高也是底边的中线,求出三角形被分成两个等腰直角三角形,求出两底角,再根据三角形的内角和定理即可求出顶角的度数.
解答:
 解:如图,根据题意,AD=
解:如图,根据题意,AD= BC,
BC,∵△ABC是等腰三角形,且AB=AC,AD⊥BC,
∴BD=CD,
∴△ABD,△ACD是等腰直角三角形,
∴∠B=∠C=45°,
∴∠BAC=180°-45°×2=90°,
即这个等腰三角形的顶角度数是90°.
故选C.
点评:本题考查了等腰三角形三线合一的性质,等腰三角形的两底角相等的性质,作出图形形象直观,更有助于问题的解决.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
等腰三角形底边上的高等于底边的一半,则这个等腰三角形的顶角度数是( )
| A、30° | B、45° | C、90° | D、120° |
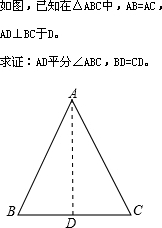 小明在证明“等腰三角形底边上的高线、底边上的中线和顶角的平分线互相重合”这一命题时,画出图形,写出“已知”、“求证”(如图).
小明在证明“等腰三角形底边上的高线、底边上的中线和顶角的平分线互相重合”这一命题时,画出图形,写出“已知”、“求证”(如图).