Question

【题目】如图，已知：∠AOB＝90°，OC平分∠AOB，点P在射线OC上．点E在射线OA上，点F在射线OB上，且∠EPF＝90°．

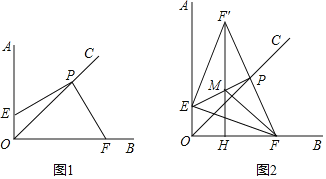
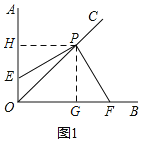
（1）如图1，求证：PE＝PF；

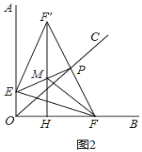
（2）如图2，作点F关于直线EP的对称点F′，过F′点作FH⊥OF于H，连接EF′，F′H与EP交于点M．连接FM，图中与∠EFM相等的角共有　 　个．

Answer 1

【答案】（1）见解析；（2）4.

【解析】

（1）过P作PG⊥OB于G，PH⊥AO于H，判定△PEH≌△PFG（AAS），即可得出PE＝PF；

（2）依据轴对称的性质以及等腰直角三角形的性质，即可得到与∠EFM相等的角．

解：（1）如图1，过P作PG⊥OB于G，PH⊥AO于H，则∠PGF＝∠PHE＝90°，

∵OC平分∠AOB，PG⊥OB，PH⊥AO，

∴PH＝PG，

∵∠AOB＝∠EPF＝90°，

∴∠PFG+∠PEO＝180°，

又∵∠PEH+∠PEO＝180°，

∴∠PEH＝∠PFG，

∴△PEH≌△PFG（AAS），

∴PE＝PF；

（2）由轴对称可得，∠EFM＝∠EF′M，

∵F′H⊥OF，AO⊥OB，

∴AO∥F′F，

∴∠EF′M＝∠AEF′，

∵∠AEF′+∠OEF＝∠OFE+∠OEF＝90°，

∴∠AEF′＝∠OFE，

由题可得，P是FF′的中点，EF＝EF′，

∴EP平分∠FEF′，

∵PE＝PF，∠EPF＝90°，

∴∠PEF＝45°＝∠PEF′，

又∵∠AOP＝∠AOB＝45°，且∠AEP＝∠AOP+∠OPE，

∴∠AEF′+45°＝45°+∠OPE，

∴∠AEF′＝∠OPE，

∴与∠EFM相等的角有4个：∠EF′M，∠AEF′，∠EFO，∠EPO．

故答案为：4．