题目内容
如图,CD切⊙于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为10。Sin∠COD=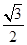 。
。
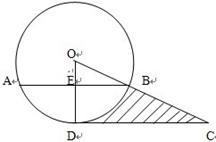
求:①弦AB的长;
②阴影部分面积
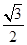 。
。
求:①弦AB的长;
②阴影部分面积
①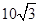 ②
②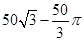
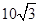 ②
②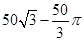
解:(1)∵AB⊥OD,在Rt△OEB中,sin∠COD=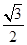
∴ ,OB=10,
,OB=10,
∴EB=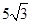
∴AB=2EB=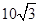
(2)∵sin∠COB=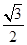
∴∠COB=60°,在Rt△COD中,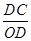 =tan60°=
=tan60°=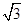
∴DC=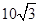
∴△ODC的面积=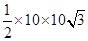 =
=
S扇形DOB= ∴S阴影=
∴S阴影= 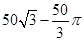
①利用Sin∠COD=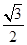 ,已知OD=10,所以BE=
,已知OD=10,所以BE=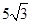 ,所以AB=
,所以AB=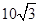 ;
;
②根据△ODC的面积- S扇形DOB即可求得
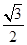
∴
 ,OB=10,
,OB=10,∴EB=
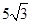
∴AB=2EB=
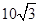
(2)∵sin∠COB=
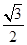
∴∠COB=60°,在Rt△COD中,
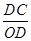 =tan60°=
=tan60°=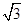
∴DC=
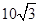
∴△ODC的面积=
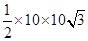 =
=
S扇形DOB=
 ∴S阴影=
∴S阴影= 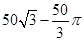
①利用Sin∠COD=
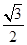 ,已知OD=10,所以BE=
,已知OD=10,所以BE=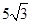 ,所以AB=
,所以AB=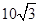 ;
;②根据△ODC的面积- S扇形DOB即可求得

练习册系列答案
相关题目
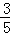 .如图,把△ABC的一边BC放置在x轴上,有OB=14,OC=
.如图,把△ABC的一边BC放置在x轴上,有OB=14,OC= ,AC与y轴交于点E.
,AC与y轴交于点E.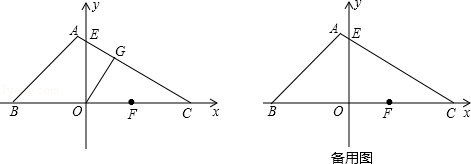
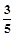 ,tan37°=
,tan37°=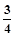 ,sin48°=
,sin48°=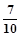 ,tan48°=
,tan48°=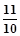 )
)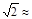 1.414,
1.414,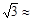 1.732)
1.732)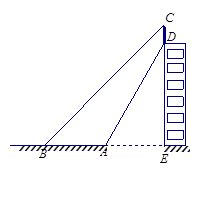
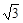 ≈1.732,结果保留整数).
≈1.732,结果保留整数).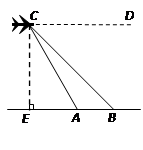
 .
.