题目内容
【题目】如图,四边形OABC为矩形,以点O为原点建立直角坐标系,点C在x轴的正半轴上,点A在y轴的正半轴上,反比例函数y=![]() 图象经过AB的中点D(1,3),且与BC交于点E,设直线DE的解析式为y=mx+n.
图象经过AB的中点D(1,3),且与BC交于点E,设直线DE的解析式为y=mx+n.
(1)求k的值和点E的坐标;
(2)直接写出不等式![]() -n>mx的解集;
-n>mx的解集;
(3)点Q为x轴上一点,点P为反比例函数y=![]() 图象上一点,是否存在点P、Q,使得以P、Q、D、E为顶点的四边形为平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
图象上一点,是否存在点P、Q,使得以P、Q、D、E为顶点的四边形为平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.

【答案】(1)k= 3,E(2,![]() );(2)0<x<1或x>2;(3)存在;使得以P、Q、D、E为顶点的四边形为平行四边形的P点的坐标为(-2,-
);(2)0<x<1或x>2;(3)存在;使得以P、Q、D、E为顶点的四边形为平行四边形的P点的坐标为(-2,-![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)将D的坐标,代入反比例函数的解析式可求得k的值,然后求得点E的纵坐标,然后将点E的横坐标代入反比例函数的解析式可求得点E的纵坐标;
(2)不等式![]() -n>mx的解集为反比例函数图象位于直线上方部分自变量x的取值范围;
-n>mx的解集为反比例函数图象位于直线上方部分自变量x的取值范围;
(3)分为ED为平行四边形的一边和DE为平行四边形的对角线两种情况列方程求解即可.
解:(1)k=xy=1×3=3,
∴反比例函数的解析式为y=![]() .
.
∵D是AB的中点,D(1,3),
∴E点的横坐标为2.
∴yE=![]() .
.
∴E(2,![]() ).
).
(2)∵不等式![]() -n>mx的解集为反比例函数图象位于直线上方部分自变量x的取值范围,
-n>mx的解集为反比例函数图象位于直线上方部分自变量x的取值范围,
∴不等式的解集为0<x<1或x>2.
(3)存在;
∵D(1,3),E(2,![]() ),以P、Q、D、E为顶点的四边形为平行四边形,
),以P、Q、D、E为顶点的四边形为平行四边形,
当DE是平行四边形的边时,则PQ∥DE,且PQ=DE,
∴Q的纵坐标为0,
∴P的纵坐标为±![]() ,
,
令y=![]() ,则
,则![]() =
=![]() ,解得x=2(舍去),
,解得x=2(舍去),
令y=-![]() ,则-
,则-![]() =
=![]() ,解得x=-2,
,解得x=-2,
∴P点的坐标为(-2,-![]() );
);
当DE是平行四边形的对角线时,
∵D(1,3),E(2,![]() ),
),
∴DE的中点为(![]() ,
,![]() ),
),
设P(a,![]() )、Q(x,0),
)、Q(x,0),
∴![]() ÷2=
÷2=![]() ,
,![]() =
=![]() ,解得:a=
,解得:a=![]() ,x=
,x=![]() .
.
∴P(![]() ,
,![]() ),
),
故使得以P、Q、D、E为顶点的四边形为平行四边形的P点的坐标为(-2,-![]() )或(
)或(![]() ,
,![]() ).
).

 阅读快车系列答案
阅读快车系列答案【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的重量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准重量的差值(单位:g) | ﹣5 | ﹣2 | 0 | 1 | 3 | 6 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)计算这批样品的平均重量,判断它比标准重量重还是轻多少?
(2)若标准重量为450克,则这批样品的总重量是多少?
(3)若这种食品的合格标准为450±5克,则这批样品的合格率为 (直接填写答案)
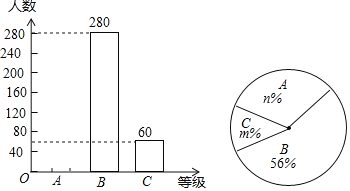
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如下图所示:

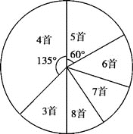
大赛结束后一个月,再次调查这部分学生“一周诗词诵背数量”,绘制成统计表:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人 数 | 10 | 10 | 15 | m | 25 | 20 |
请根据调查的信息
(1)本次调查抽取了多少名学生?
(2)补全条形统计图,在扇形统计图中,“6首”的圆心角为 度;
(3)表格中m的值为 ;
(4)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
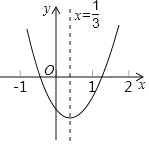
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
(1)二次函数y=ax2+bx+c 有最小值,最小值为-3;
(2)抛物线与y轴交点为(0,-3);
(3)二次函数y=ax2+bx+c 的图像对称轴是x=1;
(4)本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1