题目内容
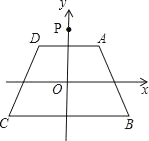
【题目】如图，在平面直角坐标系xOy中，等腰梯形ABCD的顶点坐标分别为A（1，1），B（2，﹣1），C（﹣2，﹣1），D（﹣1，1）．以A为对称中心作点P（0，2）的对称点P1，以B为对称中心作点P1的对称点P2，以C为对称中心作点P2的对称点P3，以D为对称中心作点P3的对称点P4，…，重复操作依次得到点P1，P2，…，则点P2010的坐标是（ ）
A. （2010，2） B. （2010，﹣2） C. （2012，﹣2） D. （0，2）
【答案】B
【解析】分析：根据题意，以A为对称中心作点P（0，2）的对称点P1，即A是PP1的中点，结合中点坐标公式即可求得点P1的坐标；同理可求得其它各点的坐标，分析可得规律，进而可得答案．
详解：根据题意，以A为对称中心作点P（0，2）的对称点P1，即A是PP1的中点，
又∵A的坐标是（1，1），
结合中点坐标公式可得P1的坐标是（2，0）；
同理P2的坐标是（2，﹣2），记P2（a2，b2），其中a2=2，b2=﹣2．
根据对称关系，依次可以求得：
P3（﹣4﹣a2，﹣2﹣b2），P4（2+a2，4+b2），P5（﹣a2，﹣2﹣b2），P6（4+a2，b2），
令P6（a6，b2），同样可以求得，点P10的坐标为（4+a6，b2），即P10（4×2+a2，b2），
∵2010=4×502+2，
∴点P2010的坐标是（2010，﹣2），
故选：B．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
