题目内容
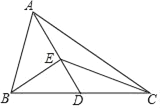
【题目】已知,如图,在△ABC中,AB=9,BC=12,点D是BC的中点,联结AD,AD=9,点E在AD边上,且![]() ,联结BE.
,联结BE.
(1)求证:△BED∽△ABD;
(2)联结CE,求∠CED 的正切值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据AD=9, ![]() ,得到AE=5,DE=4,根据中点的性质得到BD=6,即可求出
,得到AE=5,DE=4,根据中点的性质得到BD=6,即可求出![]() 得到
得到![]() 又∠ADB=∠BDE,即可证明.
又∠ADB=∠BDE,即可证明.
(2)根据![]() BD=CD,得到
BD=CD,得到![]() 又ADC=∠CDE,得到△ADC∽△CDE,根据相似三角形的性质得到∠CED=∠ACB,过A作AH⊥BD于H,
又ADC=∠CDE,得到△ADC∽△CDE,根据相似三角形的性质得到∠CED=∠ACB,过A作AH⊥BD于H,
根据勾股定理得到![]() 即可求出tan∠CED=tan∠ACB=
即可求出tan∠CED=tan∠ACB=![]()
(1)证明:∵AD=9, ![]() ,
,
∴AE=5,DE=4,
∵BC=12,点D是BC的中点,
∴BD=6,
∵![]()
∴![]()
∵∠ADB=∠BDE,
∴△BED∽△ABD;
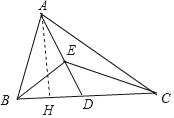
(2)∵![]() BD=CD,
BD=CD,
∴![]()
∵∠ADC=∠CDE,
∴△ADC∽△CDE,
∴∠CED=∠ACB,
过A作AH⊥BD于H,
∵AB=AD=9,
∴BH=DH=3,
∴![]()
∴tan∠CED=tan∠ACB=![]()

练习册系列答案
相关题目