题目内容
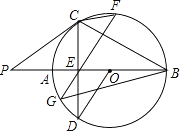
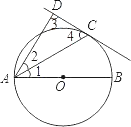
【题目】如图，已知AB是⊙O的直径，直线CD与⊙O相切于C点，AC平分∠DAB．
（1）求证：AD⊥CD；
（2）若AD＝2，AC=
，求⊙O的半径R的长．
【答案】（1）证明见解析
（2）
【解析】
试题（1）连接OC，由题意得OC⊥CD．又因为AC平分∠DAB，则∠1=∠2=
∠DAB．即可得出AD∥OC，则AD⊥CD；
（2）连接BC，则∠ACB=90°，可证明△ADC∽△ACB．则
，从而求得R．
试题解析：（1）证明：连接OC，
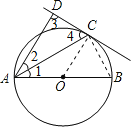
∵直线CD与⊙O相切于C点，AB是⊙O的直径，
∴OC⊥CD．
又∵AC平分∠DAB，
∴∠1=∠2=∠DAB．
又∠COB=2∠1=∠DAB，
∴AD∥OC，
∴AD⊥CD．
（2）连接BC，则∠ACB=90°，
在△ADC和△ACB中
∵∠1=∠2，∠3=∠ACB=90°，
∴△ADC∽△ACB．
∴
∴R=
练习册系列答案
相关题目
【题目】去学校食堂就餐，经常会在一个买菜窗口前等待，经调查发现，同学的舒适度指数y与等时间x（分）之间满足反比例函数关系，如下表：
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
（1）求y与x的函数关系式，并写出自变量x的取值范围．
（2）若等待时间8分钟时，求舒适度的值；
（3）舒适度指数不低于10时，同学才会感到舒适．请说明，作为食堂的管理员，让每个在窗口买菜的同学最多等待多少时间？
