题目内容
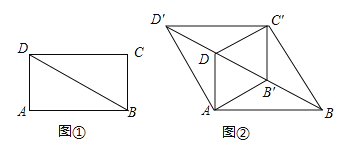
【题目】如图,在矩形纸片![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上移动,连接
上移动,连接![]() ,将多边形
,将多边形![]() 沿直线
沿直线![]() 折叠,得到多边形
折叠,得到多边形![]() ,点
,点![]() 、
、![]() 的对应点分别为点
的对应点分别为点![]() 、
、![]() .
.
(1)当![]() 恰好经过点
恰好经过点![]() 时(如图1),求线段
时(如图1),求线段![]() 的长;
的长;
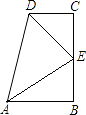
(2)若![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() (如图2),求
(如图2),求![]() 的面积;
的面积;
(3)在点![]() 从点
从点![]() 移动到点
移动到点![]() 的过程中,求点
的过程中,求点![]() 运动的路径长.
运动的路径长.

【答案】(1) ![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据折叠的性质可得![]() ,
,![]() ,
,![]() ,
,![]() ,根据勾股定理求得
,根据勾股定理求得![]() ,即可得
,即可得![]() ,易证
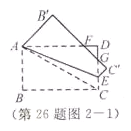
,易证![]() ,根据相似三角形的性质即可求得CE的长;(2)如图2-1,连接AC,根据锐角三角函数求得∠BAC=60°,再求得
,根据相似三角形的性质即可求得CE的长;(2)如图2-1,连接AC,根据锐角三角函数求得∠BAC=60°,再求得![]() ,根据等腰直角三角形的性质求得
,根据等腰直角三角形的性质求得![]() ,即可求得
,即可求得![]() 的面积;(3)如图2-2,连接A
的面积;(3)如图2-2,连接A![]() ,则
,则![]() ,点
,点![]() 的运动路径是以点A为圆心,以AC为半径的圆弧,根据弧长公式计算即可.
的运动路径是以点A为圆心,以AC为半径的圆弧,根据弧长公式计算即可.
试题解析:
(1)如图1,由折叠得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得,![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因![]() ,所以
,所以![]()
又![]() ,所以
,所以![]()
所以![]() ,即
,即![]() ,所以
,所以![]()
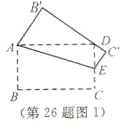
(2)如图2-1,连接AC,因为∠BAC=![]() ,所以∠BAC=60°,
,所以∠BAC=60°,
故∠DAC=30°,又![]() ,所以
,所以![]() ,
,
由折叠得,![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ;
;
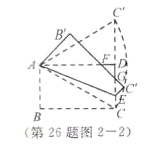
(3) 如图2-2,连接A![]() ,则
,则![]() ,
,
所以点![]() 的运动路径是以点A为圆心,以AC为半径的圆弧;当点E运动到点D时,点
的运动路径是以点A为圆心,以AC为半径的圆弧;当点E运动到点D时,点![]() 恰好在CD的延长线上,此时
恰好在CD的延长线上,此时![]() ,
,
所以点的运动路径长是![]() .
.

练习册系列答案
相关题目