题目内容
13、已知在平面直角坐标系中,点A、B的坐标分别为:A(-3,4),B(4,-2).
(1)求点A、B关于y轴对称的点的坐标;
(2)在平面直角坐标系中分别作出点A、B关于x轴的对称点M、N,顺次连接AM、BM、BN、AN,求四边形AMBN的面积.
(1)求点A、B关于y轴对称的点的坐标;
(2)在平面直角坐标系中分别作出点A、B关于x轴的对称点M、N,顺次连接AM、BM、BN、AN,求四边形AMBN的面积.
分析:(1)平面内关于y轴对称的点的坐标关系:纵坐标相同,横坐标互为相反数;
(2)根据题意,易得M,N的坐标;进而可得AM、BM、BN、AN的长;再根据有一个角是直角的平行四边形AMBN为长方形,进而可得四边形AMBN的面积.
(2)根据题意,易得M,N的坐标;进而可得AM、BM、BN、AN的长;再根据有一个角是直角的平行四边形AMBN为长方形,进而可得四边形AMBN的面积.
解答:解:(1)根据轴对称的性质,得A(-3,4)关于y轴对称的点的坐标是(3,4);
点B(4,-2)关于y轴对称的点的坐标是(-4,-2).
(2)根据题意:点M、N与点A、B关于x轴对称,可得M(-3,-4),N(4,2);
进而可得四边形AMBN为长方形,且AM=BN=8,BM=AN=4.
故四边形AMBN的面积为4×8=32.
点B(4,-2)关于y轴对称的点的坐标是(-4,-2).
(2)根据题意:点M、N与点A、B关于x轴对称,可得M(-3,-4),N(4,2);
进而可得四边形AMBN为长方形,且AM=BN=8,BM=AN=4.
故四边形AMBN的面积为4×8=32.
点评:本题考查了函数图象上的点的坐标与函数解析式的关系,以及关于y轴对称的点坐标之间的关系.

练习册系列答案
相关题目
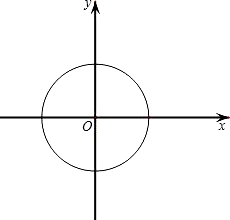 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1.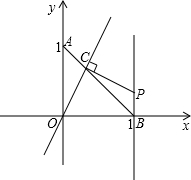 直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y),
直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y), 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.