题目内容
已知在平面直角坐标系中，点A，点B的坐标分别为A（0，0），B（0，4），点C在x轴上，且△ABC的面积为6，求点C的坐标．分析：首先求得AB的长，根据三角形的面积公式，即可求得C的横坐标，进而得到C的坐标．
解答：解：设点C坐标是（x，0）根据题意得，
AB×AC=6
即
×4×|x|=6
解得x=±3
所以点C坐标是（3，0）或（-3，0）．
| 1 |
| 2 |
即
| 1 |
| 2 |
解得x=±3
所以点C坐标是（3，0）或（-3，0）．
点评：本题考查了三角形的面积，关键是理解三角形的面积公式，把点的坐标的问题转化为三角形的高的问题．
练习册系列答案
相关题目
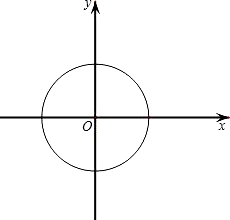已知在平面直角坐标系xOy中，⊙O的半径为1．
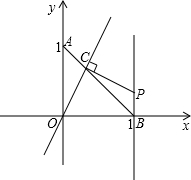直线交线段AB于点C，过点C作OC的垂线与直线x=1相交于点P，设AC=t，点P的坐标为（1，y），
如图，已知在平面直角坐标系中，平行四边形ABCD顶点A（0，0），C（10，4），直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分，求a的值．