题目内容
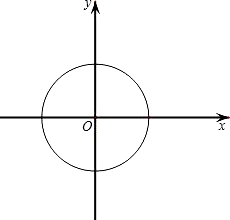 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1.(1)当直线l:y=x+b与⊙O只有一个交点时,求b的值;
(2)当反比例函数y=
| k | x |
(3)试探究当n取不同的数值时,二次函数y=x2+n的图象与⊙O交点个数情况.
分析:(1)根据已知条件得出两种符合要求的解析,利用等腰三角形的性质,分别求出即可;
(2)利用特殊点当反比例函数两曲线与圆相切时,求出DF=OF,从而得出xy的值,进而得出取值范围;
(3)根据当n>1时,有0个交点;②当n=1时,有1个交点;③当-1<n<1时,有2个交点;④当n=-1时,有3个交点;
⑤当-1.25<n<-1时,有4个交点;⑥当n=-1.25时,⑦当n<-1.25时,分别分析得出.
(2)利用特殊点当反比例函数两曲线与圆相切时,求出DF=OF,从而得出xy的值,进而得出取值范围;
(3)根据当n>1时,有0个交点;②当n=1时,有1个交点;③当-1<n<1时,有2个交点;④当n=-1时,有3个交点;
⑤当-1.25<n<-1时,有4个交点;⑥当n=-1.25时,⑦当n<-1.25时,分别分析得出.
解答: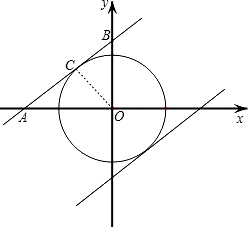 解:(1)∵y=x+b与⊙O只有一个交点,
解:(1)∵y=x+b与⊙O只有一个交点,
∴y=x+b与x轴,与y轴的交点坐标分别为:(±b,0),(0,±b),
∴△AOB为等腰直角三角形,CO=AC=BC=1,
∴b的值为:b=±
;
(2)∵反比例函数y=
的图象与⊙O有四个交点,
∵当图象与与⊙O有二个交点时,
曲线与圆相切,得出DF=OF=
,
∴xy=k=
,
∴-
<k<
(k≠0);
(3)①当n>1时,有0个交点;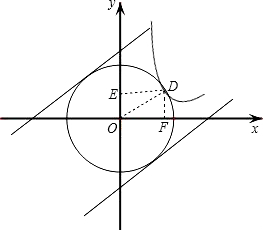
②当n=1时,有1个交点;
③当-1<n<1时,有2个交点;
④当n=-1时,有3个交点;
⑤当-1.25<n<-1时,有4个交点;
⑥当n=-1.25时,有2个交点;
⑦当n<-1.25时,有0个交点;
简解:∵x2+y2=1而y=x2+n即x2=y-n,
代入得y-n+y2=1,即y2+y-n-1=0,
要使二次函数图象与下半圆只有两个交点,根据对称性,y必须唯一,
∴△=4n+5=0,n=-
.
 解:(1)∵y=x+b与⊙O只有一个交点,
解:(1)∵y=x+b与⊙O只有一个交点,∴y=x+b与x轴,与y轴的交点坐标分别为:(±b,0),(0,±b),
∴△AOB为等腰直角三角形,CO=AC=BC=1,
∴b的值为:b=±
| 2 |
(2)∵反比例函数y=
| k |
| x |
∵当图象与与⊙O有二个交点时,
曲线与圆相切,得出DF=OF=
| ||
| 2 |
∴xy=k=
| 1 |
| 2 |
∴-
| 1 |
| 2 |
| 1 |
| 2 |
(3)①当n>1时,有0个交点;

②当n=1时,有1个交点;
③当-1<n<1时,有2个交点;
④当n=-1时,有3个交点;
⑤当-1.25<n<-1时,有4个交点;
⑥当n=-1.25时,有2个交点;
⑦当n<-1.25时,有0个交点;
简解:∵x2+y2=1而y=x2+n即x2=y-n,
代入得y-n+y2=1,即y2+y-n-1=0,
要使二次函数图象与下半圆只有两个交点,根据对称性,y必须唯一,
∴△=4n+5=0,n=-
| 5 |
| 4 |
点评:此题主要考查了抛物线解析式的确定、以及反比例函数的性质和三角形面积的求法等重要知识点,此题中,都用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
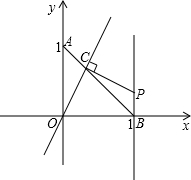 直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y),
直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y), 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.