题目内容
【题目】在学习《展开与折叠》这一课时，老师让同学们将准备好的正方体或长方体沿某些棱剪开，展开成平面图形.其中，阿中同学不小心多剪了一条棱，把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识，回答下列问题：
（1）阿中总共剪开了几条棱？
（2）现在阿中想将剪断的图②重新粘贴到图①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，他有几种粘贴方法？请在图①上画出粘贴后的图形（画出一种即可）；
（3）已知图③是阿中剪开的图①的某些数据，求这个长方体纸盒的体积.
【答案】（1）8条；（2）有4种粘贴方法，图形见解析；（3）这个长方形纸盒的体积为
【解析】
(1)长方体共有12条棱，图①中未剪的棱有4条，由此可得出剪开的棱数；
(2)根据长方体的展开图直接复原即可，注意两个相对面中间要隔一个面；
(3)直接设长方体的高为x，则根据图中数据可得出长、宽的代数式，从而解得x的值，再求体积即可.
解：(1)12-4=8(条)
因此，阿中总共剪开了8条棱.
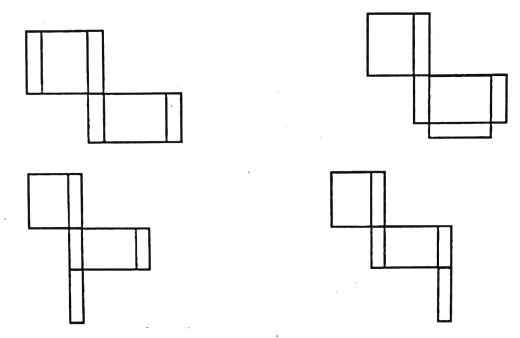
(2)有4种粘贴方法.
如图，四种情况：
(3)设高为
，则宽为
，长为
∴
解得：
∴体积为：
答：这个长方形纸盒的体积为.
练习册系列答案
相关题目
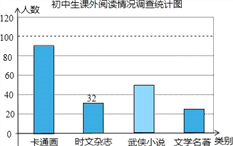
【题目】某校随机调查了部分学生，就“你最喜欢的图书类别”（只选一项）对学生课外阅读的情况作了调查统计，将调查结果统计后绘制成如下统计表和条形统计图，请根据统计图表提供的信息解答下列问题：
种类 | 频数 | 频率 |
卡通画 | a | 0.45 |
时文杂志 | b | 0.16 |
武侠小说 | 50 | c |
文学名著 | d | e |
（1）这次随机调查了 名学生，统计表中d= ；
（2）假如以此统计表绘出扇形统计图，则武侠小说对应的圆心角是 ；
（3）试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍？
