题目内容
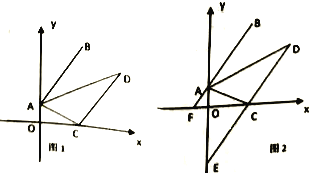
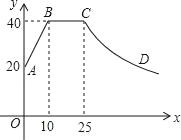
【题目】如图,过矩形![]() 的对角线
的对角线![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 边于点
边于点![]() ,交
,交![]() 边于点
边于点![]() ,分别连接
,分别连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )

A. ![]() B. 4C.
B. 4C. ![]() D. 6
D. 6
【答案】B
【解析】
求出∠ACB=∠DAC,然后利用“角角边”证明△AOF和△COE全等,根据全等三角形对应边相等可得OE=OF,再根据对角线互相垂直平分的四边形是菱形得到四边形AECF是菱形,再求出∠ECF=60°,然后判断出△CEF是等边三角形,根据等边三角形的三条边都相等可得EF=CF,根据矩形的对边相等可得CD=AB,然后求出CF,从而得解.
∵矩形对边AD∥BC,
∴∠ACB=∠DAC,
∵O是AC的中点,
∴AO=CO,
在△AOF和△COE中,
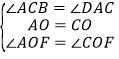 ,
,
∴△AOF≌△COE(ASA),
∴OE=OF,
又∵EF⊥AC,
∴四边形AECF是菱形,
∵∠DCF=30°,
∴∠ECF=90°-30°=60°,
∴△CEF是等边三角形,
∴EF=CF,
∵AB=![]() ,
,
∴CD=AB=![]() ,
,
∵∠DCF=30°,
∴DF=![]() ,
,
∴CF2=DF2+CD2,即![]() ,
,
∴CF=4,
∴EF=4.
故选B.

 名校课堂系列答案
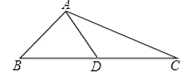
名校课堂系列答案【题目】如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.

【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成不完整的统计表与统计图,请结合图中的信息解答下列问题.
学生最喜欢的图书类别人数统计表
图书类别 | 画记 | 人数 | 百分比 |
文学类 | |||
艺体类 | 正 | 5 | |
科普类 | 正正一 | 11 | 22% |
其它 | 正正 | 14 | 28% |
合计 | a | 100% |


(1)随机抽取的样本容量a为_________________________;
(2)补全扇形统计图和条形统计图;
(3)已知该校有600名学生,估计全校最喜欢文学类图书的学生人数.