Question

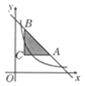
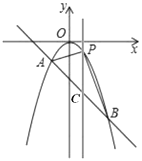
【题目】如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c(a>0)与x轴的正半轴交于A，C两点(点A在点C右侧)，与y轴正半轴交于点B，连结BC，将△BOC沿直线BC翻折，若点O恰好落在线段AB上，则称该抛物线为”折点抛物线”，下列抛物线是“折点抛物线”的是( )

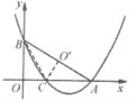
A.B.

C.D.

Answer 1

【答案】B

【解析】

观察函数图像，可知抛物线与x轴有两个交点，则b2-4ac＞0，因此可以排除A；再由B选项中的y=0，解关于x的方程，求出x的值，可得到点A，C的坐标，从而可求出AC的长，由题意可知OC=O'C=1，OB=O'B=3，再利用勾股定理求出AB的长，即可得到AO'的长，然后利用勾股定理的逆定理进行验证，可得答案，或求出一次函数BA的解析式，再求出点O'的坐标，将点O'的横坐标代入函数解析式，求出其纵坐标，即可得出答案.

A. 当y=0时，

∴9x2-33x+32=0

b2-4ac=332-4×9×32=-63＜0，

∴抛物线与x轴无交点，故A不符合题意；

B. 当y=0时，

解得x1=1，x2=

∴A(，0)，C(1，0)

当x=0时，y=3

∴点B(0，3)

∵将△BOC沿直线BC翻折，若点O恰好落在线段AB上，

∴OC=O'C=1，OB=O'B=3

在Rt△ABO中，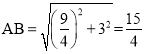

∴AO'=

又∵AC=

∵，

∴

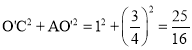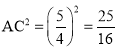
∴∠AO'C=90°=∠BO'C

∴B、O'、A三点共线

∴将△BOC沿直线BC翻折，点O恰好落在线段AB上，

∴“折点抛物线”为

同理可判断C、D均不是“折点抛物线”.

故选B.