题目内容
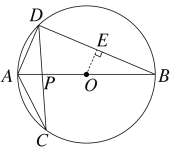
【题目】如图，在⊙O中，直径AB与弦CD相交于点P，∠CAB=62°,∠APD=86°.
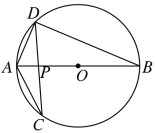
(1)求∠B的大小；
(2)已知AD=6，求圆心O到BD的距离.
【答案】(1)∠B=24°；(2)点O到BD的距离为3.
【解析】
(1)利用三角形的一个外角等于和它不相邻的两内角之和，可求出∠C的度数，再利用同弧所对的圆周角相等，求出∠B的度数.
(2)过点O作OE⊥BD于点E，利用垂径定理可得点E是BD的中点，再利用圆周角定理可得AD⊥BD，从而可证OE是△ADB的中位线，然后利用三角形中位线定理可求出结果.
解：(1)∵∠APD=∠C+∠CAB,
∴∠C=86°-62°=24°
∴∠B=∠C=24°
(2)过点O作OE⊥BD于点E
∴DE=BE，
∵AB是直径，
∴∠ADB=90°，即AD⊥BD
∴OE∥AD，点E是BD的中点，点O是AB的中点
∴OE是△ADB的中位线，
∴
∴点O到BD的距离为3.
练习册系列答案
相关题目
