题目内容
【题目】在正方形ABCD和正方形AEFG中,点B在边AG上,点D在线段EA的延长线上,连接BE.
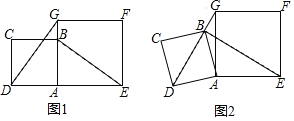
(1)如图1,求证:DG⊥BE;
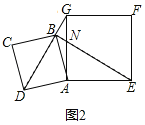
(2)如图2,将正方形ABCD绕点A按逆时针方向旋转,使点B恰好落在线段DG上.
①求证:DG⊥BE;
②若AB=2,AG=3,求线段BE的长.
【答案】(1)见解析;(2)①见解析;②BE=![]() .
.
【解析】
(1)延长EB,交DG于H,先证△DAG≌△BAE,即可得到∠DGA=∠BEA,再证∠DHE=90°即可;
(2)①原理同(1);
②连接AC,交DG于点M,由正方形的对角线互相垂直平分即可求出AM=DM,再根据勾股定理即可求出MG从而求出DG,再根据①中全等即可得到线段BE的长.
(1)证明:延长EB,交DG于H,如图1所示:
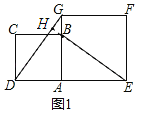
∵四边形ABCD和四边形AEFG是正方形,
∴AD=AB,AG=AE,∠DAG=∠BAE=90°,
在△DAG和△BAE中 ,
,
∴△DAG≌△BAE (SAS)
∴∠DGA=∠BEA,
又∵∠DGA+∠GDA=90°,
∴∠BEA+∠GDA=90°,
∴∠DHE=90°,
∴DG⊥BE;
(2)①证明:设AG交BE于N,如图2所示:
由旋转的性质得:∠BAD=90°,AB=AD,
∵∠BAD=90°,∠GAE=90°,
∴∠BAD+∠BAG=∠GAE+∠BAG,
即∠DAG=∠BAE,
在△DAG和△BAE中,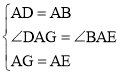 ,
,
∴△DAG≌△BAE (SAS),
∴∠AGD=∠AEB,
又∵∠BNG=∠ANE,
∴∠GBE=∠GAE=90°,
∴DG⊥BE;
②解:如图3,连接AC,交DG于点M,
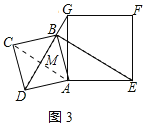
∵四边形ABCD是正方形,AB=2,
∴AC⊥BD,AD=AB=2,且△ADM是等腰直角三角形,
∴AM=DM=![]() AD=
AD=![]() ,
,
在Rt△AMG中,![]() ,
,
∴![]() ,
,
由①知,△DAG≌△BAE,
∴![]() .
.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目