题目内容
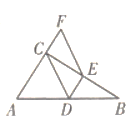
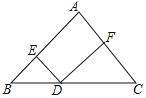
【题目】如图，在△ABC中，AB＝AC＝10，BC＝12，点D是BC上一点，DE∥AC，DF∥AB，则△BED与△DFC的周长的和为（ ）
A. 34B. 32C. 22D. 20
【答案】B
【解析】
首先根据两组对边互相平行的四边形是平行四边形判定出四边形AEDF是平行四边形，进而得到DF＝AE，然后证明DE＝BE，即可得到DE+DF＝AB，从而得解．
解：∵DE∥AC，DF∥AB，
∴四边形AEDF是平行四边形，
∴DF＝AE，
又∵DE∥AC，
∴∠C＝∠EDB，
又∵AB＝AC，
∴∠B＝∠C，
∴∠B＝∠EDB，
∴DE＝BE，
∴DF+DE＝AE+BE，
∴△BED与△DFC的周长的和＝△ABC的周长＝10+10+12＝32，
故选：B．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
