题目内容
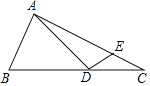
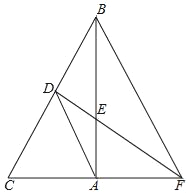
【题目】如图,在△ABC中,∠BAC=90°,BC的垂直平分线交BC于D,交AB于E,交CA的延长线于F.求证:AD2=DEDF.
【答案】证明见解析
【解析】
利用直角三角形的性质以及等腰三角形的性质可以推导得出∠DAB=∠AFD,再结合∠ADE=∠FDA可得△ADE∽△FDA,根据相似三角形对应边成比例即可得出答案.
∵∠BAC=90°,
∴∠ABC+∠C=90°,∠EAF=180°-∠BAC=90°,
∴∠AEF+∠AFE=90°,
又∵BC的垂直平分线交BC于点D,
∴∠BDE=90°,
∴∠ABC+∠BED=90°,
∵∠BED=∠AEF,
∴∠ABC=∠AFE,
∵D为BC中点,∠BAC=90°,
∴∠ABC=∠DAE,
∴∠DAE=∠AFE,
又∵∠ADE=∠FDA,
∴△ADE∽△FDA,
∴AD:FD=DE:AD,
∴AD2=DEDF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目