题目内容
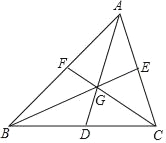
【题目】如图,点D、E、F分别为△ABC三边的中点,如果△ABC的面积为S,那么以AD、BE、CF为边的三角形的面积是_____.
【答案】![]()
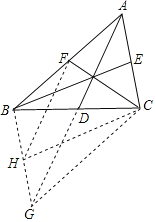
【解析】分析:延长AD至G,使得DG=AD,连接BG,CG,取BG的中点H,连接CH,FH,依据三角形中线、中位线的性质以及平行四边形的性质,即可得到△CHG的面积=△BCG的面积的一半=平行四边形ABGC的面积的![]() =
=![]() S,△BFH的面积=△ABG的面积的
S,△BFH的面积=△ABG的面积的![]() =
=![]() S,△ACF的面积=
S,△ACF的面积=![]() S,进而得出△CFH的面积=2S﹣
S,进而得出△CFH的面积=2S﹣![]() S﹣
S﹣![]() S﹣
S﹣![]() S=
S=![]() S.
S.
详解:
如图所示,延长AD至G,使得DG=AD,连接BG,CG,则△ACD≌△GBD,△ABD≌△GCD,四边形ABGC为平行四边形,
∴四边形ABGC的面积=2S,
取BG的中点H,连接CH,FH,则BH∥CE,BH=CE,故四边形BHCE是平行四边形,
∴BE=CH,
由题可得,FH是△ABG的中位线,
∴FH=![]() AG=AD,
AG=AD,
∴△CFH即为以AD、BE、CF为边的三角形,
∵△CHG的面积=△BCG的面积的一半=平行四边形ABGC的面积的![]() =
=![]() S,
S,
△BFH的面积=△ABG的面积的![]() =
=![]() S,
S,
△ACF的面积=![]() S,
S,
∴△CFH的面积=2S﹣![]() S﹣
S﹣![]() S﹣
S﹣![]() S=
S=![]() S,
S,
故答案为:![]() S.
S.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目