��Ŀ����
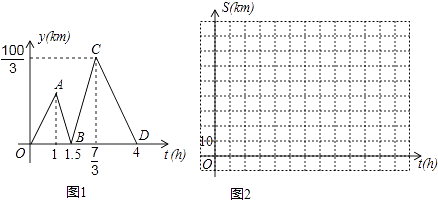
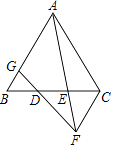
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ����3��0������0��6��������P�ӵ�O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����C�ӵ�B������������BO������ÿ��2����λ���ٶ��˶�����CP��COΪ�ڱ߹���PCOD�����߶�OP�ӳ�����ȡ��E��ʹPE=AO�����P�˶���ʱ��Ϊt�룮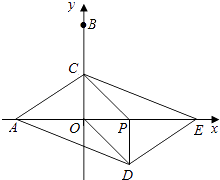
��1������C�˶����߶�OB���е�ʱ����t��ֵ����E�����ꣻ
��2������C���߶�OB��ʱ����֤���ı���ADECΪƽ���ı��Σ�
��3�����߶�PE��ȡ��F��ʹPF=1������F��MN��PE����ȡFM=2��FN=1���ҵ�M��N�ֱ���һ�������ޣ����˶������У���PCOD�����ΪS��
�ٵ���M��N����һ�������ı���ADEC�ı���ʱ�������������������t��ֵ��
������M��N��ǡ��ֻ��һ���������ı���ADEC���ڲ����������߽磩ʱ��ֱ��д��S��ȡֵ��Χ��
���𰸡�
��1��
�⣺��OB=6��C��OB���е㣬
��BC= ![]() OB=3��
OB=3��
��2t=3��t= ![]() ��
��
��OE= ![]() +3=
+3= ![]() ��E��
��E�� ![]() ��0��
��0��
��2��
�⣺��ͼ������CD��OP�ڵ�G��
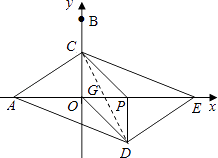
��PCOD��CG=DG��OG=PG��
��AO=PE��
��AG=EG��
���ı���ADEC��ƽ���ı��Σ�
��3��
�⣺�٣�����C��BO��ʱ��
��һ���������ͼ������M��CE����ʱ��
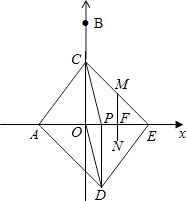
��MF��OC��
���EMF�ס�ECO��
�� ![]() ����
���� ![]() =
= ![]() ��
��
��t=1��
�ڶ������������N��DE��ʱ��
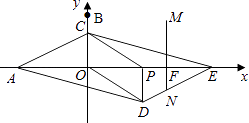
��NF��PD��
���EFN�ס�EPD��
�� ![]() ����
���� ![]() =
= ![]() ��
��
��t= ![]() ��
��
������C��BO���ӳ�����ʱ��
��һ�����������M��DE����ʱ��
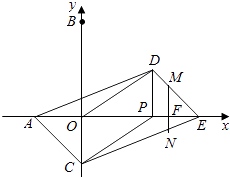
��MF��PD��
���EMF�ס�EDP��
�� ![]() ��
�� ![]() =
= ![]() ��
��
��t= ![]() ��
��
�ڶ������������N��CE����ʱ��
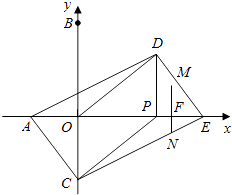
��NF��OC��
���EFN�ס�EOC��
�� ![]() ��
�� ![]() =
= ![]() ��
��
��t=5��
�� ![]() ��S��
��S�� ![]() ��
�� ![]() ��S��20��
��S��20��
��1��t�� ![]() ʱ��
ʱ��
S=t��6��2t��=��2��t�� ![]() ��2+
��2+ ![]() ��
��
��t= ![]() ��1��t��
��1��t�� ![]() ��Χ�ڣ�
��Χ�ڣ�
�� ![]() ��S��
��S�� ![]() ��
��
�� ![]() ��t��5ʱ��S=t��2t��6��=2��t��
��t��5ʱ��S=t��2t��6��=2��t�� ![]() ��2��
��2�� ![]() ��
��
�� ![]() ��S��20��
��S��20��
����������1����C��OB���е����ʱ�䣬�������E�����꣬��2������CD��OP�ڵ�G����PCOD�ĶԽ�����ȣ����ı���ADEC��ƽ���ı��Σ���3������C��BO��ʱ����һ�����������M��CE����ʱ���ɡ�EMF�ס�ECO��⣬�ڶ������������N��DE����ʱ���ɡ�EFN�ס�EPD��⣻����C��BO���ӳ�����ʱ����һ�����������M��DE����ʱ����EMF�ס�EDP��⣬�ڶ������������N��CE����ʱ���ɡ�EFN�ס�EOC��⣻�ڵ�1��t�� ![]() ʱ�͵�
ʱ�͵� ![]() ��t��5ʱ���ֱ����S��ȡֵ��Χ��
��t��5ʱ���ֱ����S��ȡֵ��Χ��
�����㾫����������Ĺؼ������������������ε�Ӧ�õ����֪ʶ�����ղ�ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������⣮