��Ŀ����
�Ķ����ϲ��ش����⣺���ϣ���a=
| 2007 |
| 2008 |
| 2008 |
| 2009 |
�⣺��a=
| 2007��2009 |
| 2008��2009 |
| (2008-1)(2008+1) |
| 2008��2009 |
| 20082-12 |
| 2008��2009 |
b=
| 2008��2008 |
| 2009��2008 |
| 20082 |
| 2008��2009 |
�֡�20082-12��20082���ҷ�ĸ��ͬ��
��a��b��
���⣺��1����գ�
| 2008 |
| 2009 |
| 2009 |
| 2010 |
��2����n��0ʱ���������ķ������Ƚ�
| n |
| n+1 |
| n+1 |
| n+2 |
�������ֱ�������������ʽ����Ϊͬ��ĸ�������ʽ�����Ӵ������ʽ�Ӿʹ�
����⣺��1����
=
=
��
=
��
��20092-12��20092���ҷ�ĸ��ͬ��
��
��
��
��2��
=
=
��
=
=
��
�߷�ĸ��ͬ��n2+2n��n2+2n+1��
��
��
��
| 2008 |
| 2009 |
| 2008��2010 |
| 2009��2010 |
| 20092 -1 |
| 2009��2010 |
| 2009 |
| 2010 |
| 20092 |
| 2009��2010 |
��20092-12��20092���ҷ�ĸ��ͬ��
��
| 2008 |
| 2009 |
| 2009 |
| 2010 |
��2��
| n |
| n+1 |
| n(n+2) |
| (n+1)(n+2) |
| n2 +2n |
| (n+1)(n+2) |
| n+1 |
| n+2 |
| (n+1)2 |
| (n+2)(n+1) |
| n2 +2n+1 |
| (n+1)(n+2) |
�߷�ĸ��ͬ��n2+2n��n2+2n+1��
��
| n |
| n+1 |
| n+1 |
| n+2 |
�������õ���֪ʶ��Ϊ����������������ĸ��ͬ�����Ӵ�����ʹ�

��ϰ��ϵ�д�
�����Ŀ

 ��x1+x2=-
��x1+x2=- ��x1x2=-
��x1x2=-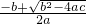 ��x2=
��x2=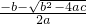 ��
�� ��b=
��b= ���Ƚ�a��b�Ĵ�С��
���Ƚ�a��b�Ĵ�С��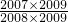 =
=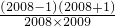 =
=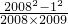 ��
��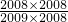 =
=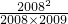 ��
��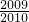 �����=�����ţ�
�����=�����ţ�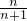 ��
��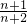 �Ĵ�С��
�Ĵ�С��