��Ŀ����
25���Ķ����ϲ��ش����⣺
����֪������ȫƽ��ʽ������ƽ�漸��ͼ�ε��������ʾ��ʵ���ϻ���һЩ�������ʽҲ������������ʽ��ʾ���磺��2a+b����a+b��=2a2+3ab+b2���Ϳ�����ͼ��1����ͼ��2����ͼ�ε������ʾ��

��1����д��ͼ��3������ʾ�Ĵ������ʽ��
��2���Ի�һ������ͼ�Σ�ʹ���������ʾ����a+b����a+3b��=a2+4ab+3b2��
��3�����������������дһ������a��b�Ĵ������ʽ��������������Ӧ�ļ���ͼ�Σ�
����֪������ȫƽ��ʽ������ƽ�漸��ͼ�ε��������ʾ��ʵ���ϻ���һЩ�������ʽҲ������������ʽ��ʾ���磺��2a+b����a+b��=2a2+3ab+b2���Ϳ�����ͼ��1����ͼ��2����ͼ�ε������ʾ��

��1����д��ͼ��3������ʾ�Ĵ������ʽ��
��2a+b����a+2b��=2a2+5ab+2b2
����2���Ի�һ������ͼ�Σ�ʹ���������ʾ����a+b����a+3b��=a2+4ab+3b2��
��3�����������������дһ������a��b�Ĵ������ʽ��������������Ӧ�ļ���ͼ�Σ�
���������⿼����ƽ�漸��ͼ�ε��������ʾһЩ�������ʽ����ͼ��3���г����ε����=������=��2a+b����a+2b���������ε���������Ѽ���Сͼ�ε������ӣ���a2+a2+ab+ab+ab+ab+ab+b2+b2=2a2+5ab+2b2��
����⣺��1����2a+b����a+2b��=2a2+5ab+2b2��
��2�� ���𰸲�Ψһ����
���𰸲�Ψһ����
��3�����ʽ�ǣ�a+2b����a+b��=a2+3ab+2b2����ͼ��ʾ��
���𰸲�Ψһ��

��2��
 ���𰸲�Ψһ����
���𰸲�Ψһ������3�����ʽ�ǣ�a+2b����a+b��=a2+3ab+2b2����ͼ��ʾ��
���𰸲�Ψһ��

��������������ȫƽ����ʽ��Ӧ�ã�������ƽ���ͣ��ټ��ϻ��ȥ���ǻ���2����������һ����ȫƽ��ʽ��ע�����2���ķ��ţ�����©�⣮

��ϰ��ϵ�д�
�����Ŀ
 ��x1+x2=-
��x1+x2=- ��x1x2=-
��x1x2=-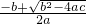 ��x2=
��x2=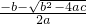 ��
�� ��b=
��b= ���Ƚ�a��b�Ĵ�С��
���Ƚ�a��b�Ĵ�С��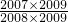 =
=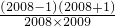 =
=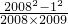 ��
��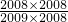 =
=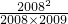 ��
��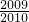 �����=�����ţ�
�����=�����ţ�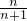 ��
��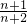 �Ĵ�С��
�Ĵ�С��