题目内容
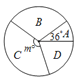
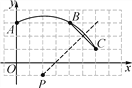
【题目】如图，在平面直角坐标系中，一段圆弧经过格点A、B、C.(网格小正方形边长为1)
(1)请写出该圆弧所在圆的圆心P的坐标，并求⊙P的半径(结果保留根号)；
(2)判断点M(－1，1)与⊙P的位置关系．
【答案】（1）2
（2）点M在⊙P内
【解析】试题分析：（1）根据垂径定理的推论：弦的垂直平分线必过圆心，可作弦AB和BC的垂直平分线，交点即为圆心然后根据勾股定理求出即可；
（2）根据勾股定理求出PM的长，然后和半径比较即可.
试题解析：(1)根据垂径定理的推论：弦的垂直平分线必过圆心，可以作弦AB和BC的垂直平分线，交点即为圆心P，如图所示．
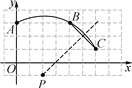
则圆心P的坐标为(2，－1)，
r＝
＝2
.
(2)∵PM＝
＜2
，
∴点M在⊙P内．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
