题目内容
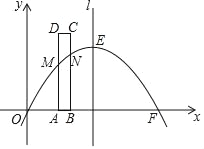
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).
(1)求该抛物线的解析式;
(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;
(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

【答案】(1)y=x2﹣2x﹣3;(2)M(﹣![]() ,﹣
,﹣![]() );(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,P的坐标为(1+
);(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,P的坐标为(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3).
,3)或(2,﹣3).
【解析】
(1)把A,B,C的坐标代入抛物线解析式求出a,b,c的值即可;
(2)由题意得到直线BC与直线AM垂直,求出直线BC解析式,确定出直线AM中k的值,利用待定系数法求出直线AM解析式,联立求出M坐标即可;
(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,分两种情况,利用平移规律确定出P的坐标即可.
(1)把A(3,0),B(﹣1,0),C(0,﹣3)代入抛物线解析式得: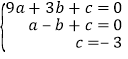 ,
,
解得: ,
,
则该抛物线解析式为y=x2﹣2x﹣3;
(2)设直线BC解析式为y=kx﹣3,
把B(﹣1,0)代入得:﹣k﹣3=0,即k=﹣3,
∴直线BC解析式为y=﹣3x﹣3,
∴直线AM解析式为y=![]() x+m,
x+m,
把A(3,0)代入得:1+m=0,即m=﹣1,
∴直线AM解析式为y=![]() x﹣1,
x﹣1,
联立得: ,
,
解得: ,
,
则M(﹣![]() ,﹣
,﹣![]() );
);
(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,
分两种情况考虑:
设Q(x,0),P(m,m2﹣2m﹣3),
当四边形BCQP为平行四边形时,由B(﹣1,0),C(0,﹣3),
根据平移规律得:﹣1+x=0+m,0+0=﹣3+m2﹣2m﹣3,
解得:m=1±![]() ,x=2±
,x=2±![]() ,
,
当m=1+![]() 时,m2﹣2m﹣3=8+2
时,m2﹣2m﹣3=8+2![]() ﹣2﹣2
﹣2﹣2![]() ﹣3=3,即P(1+
﹣3=3,即P(1+![]() ,3);
,3);
当m=1﹣![]() 时,m2﹣2m﹣3=8﹣2
时,m2﹣2m﹣3=8﹣2![]() ﹣2+2
﹣2+2![]() ﹣3=3,即P(1﹣
﹣3=3,即P(1﹣![]() ,3);
,3);
当四边形BCPQ为平行四边形时,由B(﹣1,0),C(0,﹣3),
根据平移规律得:﹣1+m=0+x,0+m2﹣2m﹣3=﹣3+0,
解得:m=0或2,
当m=0时,P(0,﹣3)(舍去);当m=2时,P(2,﹣3),
综上,存在以点B,C,Q,P为顶点的四边形是平行四边形,P的坐标为(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3).
,3)或(2,﹣3).

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案