题目内容
【题目】如图，已知AB是⊙O的直径，弦CD与AB交于点E，F为CD的延长线上一点，连接AF，且FA2=FDFC．
（1）求证：FA为⊙O的切线；
（2）若AC=8，CE：ED=6：5，AE：EB=2：3，求AB的值．
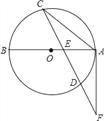
【答案】(1)见解析;(2)10
【解析】分析：
详解：(1)证明：连接BD、AD，如图，
∵
∴
∵∠F=∠F，
∴△FAD∽△FCA.
∴∠DAF=∠C.
∵∠DBA=∠C，
∴∠DBA=∠DAF.
∵AB是⊙O的直径，
∴
∴
∴
∴
即AF⊥AB.
∴FA为⊙O的切线.
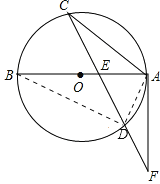
(2)设CE=6x，AE=2y，则ED=5x，EB=3y.
由相交弦定理得：ECED=EBEA.
∴
∴
∴
∵
∴
∴
∴
∴FD=5x.
∴
∴
∵
∴
∵△FAD∽△FCA.
∴
∵
∴
解得：
∴
∴AB的值为10.
练习册系列答案
阳光课堂课时作业系列答案
相关题目
