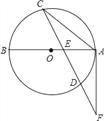
题目内容
【题目】在学校科技周活动中,丛明和蔡智同学制作的智能小车![]() ,
,![]() 做圆周(等分为
做圆周(等分为![]() 格)运动,规定顺时针方向为负运动,逆时针方向为正运动.若两小车
格)运动,规定顺时针方向为负运动,逆时针方向为正运动.若两小车![]() ,
,![]() 从
从![]() 点同时出发,当它们按
点同时出发,当它们按![]() 的速度运动到
的速度运动到![]() 秒时,共行
秒时,共行![]() 格.
格.
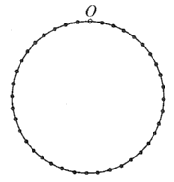
(1)求两小车的运动速度;若![]() 作正运动,
作正运动,![]() 作负运动,标出小车运动到
作负运动,标出小车运动到![]() 秒时的位置
秒时的位置![]() ,
,![]() ;
;
(2)若![]() ,
,![]() 从(1)中的位置同时出发,都沿正方向运动,再经多久时
从(1)中的位置同时出发,都沿正方向运动,再经多久时![]() ,
,![]() 所到达位置表示的数互为相反数?
所到达位置表示的数互为相反数?
(3)若![]() ,
,![]() 从(2)中的位置同时出发相向运动,当它们在
从(2)中的位置同时出发相向运动,当它们在![]() 点相遇时,
点相遇时,![]() 点所对应的数是多少?
点所对应的数是多少?
(4)若![]() ,
,![]() 从(3)中的位置同时出发,都沿负方向运动,经过多长时间
从(3)中的位置同时出发,都沿负方向运动,经过多长时间![]() ,
,![]() 首次相遇?
首次相遇?
【答案】(1)见解析;(2)再经过![]() 秒
秒![]() ,
,![]() 表示的数互为相反数;(3)1.5;(4)经过
表示的数互为相反数;(3)1.5;(4)经过![]() 秒后
秒后![]() ,
,![]() 两小车首次相遇
两小车首次相遇
【解析】
(1)先求出![]() ,
,![]() 的速度之和,由A、
的速度之和,由A、![]() 的速度比是
的速度比是![]() 求得A、B的速度,再由运动路程=速度
求得A、B的速度,再由运动路程=速度![]() 时间以及
时间以及![]() 作正运动,
作正运动,![]() 作负运动,标出小车运动到
作负运动,标出小车运动到![]() 秒时的位置
秒时的位置![]() ,
,![]() 即可;
即可;
(2)设再经过![]() 秒
秒![]() ,
,![]() 所到达位置表示的数互为相反数,据此列一元一次方程,解之即可;
所到达位置表示的数互为相反数,据此列一元一次方程,解之即可;
(3)由(2)知![]() ,
,![]() 之间的距离为
之间的距离为![]() .设经过
.设经过![]() 秒
秒![]() ,
,![]() 在
在![]() 点相遇,据此列一元一次方程,解之即可;
点相遇,据此列一元一次方程,解之即可;
(4)设经过![]() 秒
秒![]() ,
,![]() 两小车首次相遇,据此列一元一次方程,解之即可.
两小车首次相遇,据此列一元一次方程,解之即可.
(1)根据题意得![]() ,
,![]() 的速度和为
的速度和为![]() (格/秒)
(格/秒)
![]() ,
,![]() 的速度比是
的速度比是![]() ,
,
![]() 的速度是
的速度是![]() (格/秒),A的运动路程=1
(格/秒),A的运动路程=1![]() 2=2(格)
2=2(格)
![]() 的速度是
的速度是![]() (格/秒),B的运动路程=3
(格/秒),B的运动路程=3![]() 2=6(格)
2=6(格)
如图,

(2)
如图:
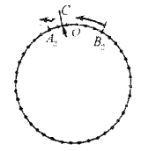
设再经过![]() 秒
秒![]() ,
,![]() 所到达位置表示的数互为相反数,
所到达位置表示的数互为相反数,
则![]() .
.
解得![]() .
.
答:再经过![]() 秒
秒![]() ,
,![]() 表示的数互为相反数.
表示的数互为相反数.
(3)由(2)知![]() ,
,![]() 所到达位置表示的数分别为
所到达位置表示的数分别为![]() 和
和![]() ,它们之间的距离为
,它们之间的距离为![]() ,
,
设经过![]() 秒
秒![]() ,
,![]() 在
在![]() 点相遇,
点相遇,
则![]() ,
,
解得![]() ,
,
![]() 点所对应的数为
点所对应的数为![]() .
.
(4)如图:

设经过![]() 秒
秒![]() ,
,![]() 两小车首次相遇,
两小车首次相遇,
则![]() .
.
解得![]() .
.
答:经过![]() 秒后
秒后![]() ,
,![]() 两小车首次相遇.
两小车首次相遇.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目