��Ŀ����
����Ŀ���κ�һ��������n�����Խ��������ķֽ⣺n=p��q��p��q������������p��q�������p��q��n���������ַֽ���������֮��ľ���ֵ��С�����Ǿͳ�p��q��p��q����n����ѷֽ⣬���涨F��n��= ![]() �����磺18���Էֽ��1��18��2��9��3��6����ʱ����F��18��=
�����磺18���Էֽ��1��18��2��9��3��6����ʱ����F��18��= ![]() =
= ![]() �����������Ϣ���������й���F��n����˵���� ��F��2��=
�����������Ϣ���������й���F��n����˵���� ��F��2��= ![]() ��
��
��F��24��= ![]() ��
��
��F��27��= ![]() ��
��
����n��һ��������ƽ������F��n��=1��
������ȷ��˵���� �� ��ֻ����ţ�
���𰸡��٢�
���������⣺��2=1��2�� ��F��2��= ![]() ����ȷ�ģ�
����ȷ�ģ�
��24=1��24=2��12=3��8=4��6���⼸�ַֽ���4��6�IJ�ľ���ֵ��С��
��F��24��= ![]() =
= ![]() ���ʢ��Ǵ���ģ�
���ʢ��Ǵ���ģ�
��27=1��27=3��9������3��9�ľ���ֵ��С����3��9��
��F��27��= ![]() ���ʢ��Ǵ���ģ�
���ʢ��Ǵ���ģ�
��n��һ����ȫƽ������
��n�ֽܷ��������ȵ�������F��n��=1���ʢ�����ȷ�ģ�
����ȷ���Т٢ܣ�
���Դ��ǣ��٢ܣ�
�����㾫�����������⣬������Ҫ�˽�������������������(��û�����ŵIJ�ͬ�������У�����˷�����˳��������Ӽ�)��

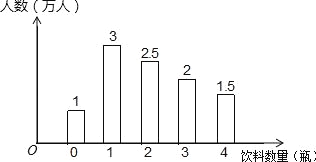
����Ŀ��ij����С��Ϊ�˽��������ο������ڹ���ƿװ���������������һ�죬���Ƿֱ���A��B��C�������ڴ������뿪�����οͽ��е��飬������A���ڵ������õ�������������ͼ
��1����A���ڵı������ο��У�����2ƿ��2ƿ�������ϵ��ο�����ռA���ڵı������ο������� 60 %��
��һ
�� �� | B | C |
�˾���������������ƿ�� | 3 | 2 |
��2������A���ڵı������ο��������˾������˶���ƿ���ϣ�
��3����֪B��C�������ڵı������ο��������˾��������ϵ��������һ��ʾ ��C���ڵı�����������B���ڵı�����������2����B��C�������ڵı������ο������ڹ�������49��ƿ���ϣ�����B���ڵı������ο�����Ϊ������