题目内容
已知关于x一元二次方程 有两个不相等的实数根
有两个不相等的实数根
(1)求k取值范围;
(2)当k最小的整数时,求抛物线 的顶点坐标以及它与x轴的交点坐标;
的顶点坐标以及它与x轴的交点坐标;
(3)将(2)中求得的抛物线在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象.请你画出这个新图象,并求出新图象与直线 有三个不同公共点时m值.
有三个不同公共点时m值.
(1)k>-1;(2)(1,-4);(-1,0),(3,0);(3)画图见解析,1或 .
.
解析试题分析:(1)根据一元二次方程 有两个不相等的实数根,可知根的判别式△>0,即可求出k的取值范围.
有两个不相等的实数根,可知根的判别式△>0,即可求出k的取值范围.
(2)根据k的取值范围可得当k=0时,为k最小的整数,进而可求出顶点坐标以及它与x轴的交点坐标.
(3)由(2)画出此函数图象后,可发现,若直线与新函数有3个交点,可以有两种情况:
①直线经过原二次函数与x轴的交点A(即左边的交点),可将A点坐标代入直线的解析式中,即可求出m的值;
②原二次函数图象x轴以下部分翻折后,所得部分图象仍是二次函数,该二次函数与原函数开口方向相反、对称轴相同、与x轴的交点坐标相同,可据此判断出该函数的解析式,若直线与新函数图象有三个交点,那么当直线与该二次函数只有一个交点时,恰好满足这一条件,那么联立直线与该二次函数的解析式,可化为一个关于x的一元二次方程,那么该方程的判别式△=0,根据这一条件可确定m的取值.
试题解析:(1)由题意,得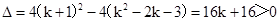 ,
,
∴k>-1,
∴k的取值范围为k>-1.
(2)∵k>-1,且k取最小的整数,∴k=0.
∴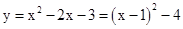 .
.
则抛物线的顶点坐标为(1,-4).
∵ 的图象与x轴相交,
的图象与x轴相交,
∴ ,∴解得:x=-1或3.
,∴解得:x=-1或3.
∴抛物线与x轴相交于A(-1,0),B(3,0);
(3)翻折后所得新图象如图所示.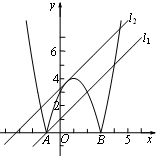
平移直线y=x+m知:直线位于l1和l2时,它与新图象有三个不同的公共点.
①当直线位于l1时,此时l1过点A(-1,0),
∴0=-1+m,即m=1.
②当直线位于l2时,此时l2与函数 的图象有一个公共点,
的图象有一个公共点,
∴方程x+m=-x2+2x+3,即x2-x-3+m=0有两个相等实根.
∴△=1-4(m-3)=0,即m= .
.
当m= 时,x1=x2=
时,x1=x2=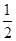 满足-1≤x≤3,
满足-1≤x≤3,
由①②知m=1或m= .
.
考点:1.抛物线与x轴的交点;2.二次函数图象与几何变换;3.一元二次方程根的判别式;4.分类思想的应用.

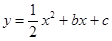 与x轴交于A,B两点,对称轴为直线
与x轴交于A,B两点,对称轴为直线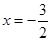 ,直线AD交抛物线于点D(2,3).
,直线AD交抛物线于点D(2,3).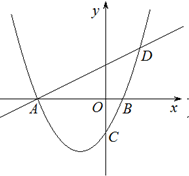
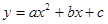 的图象过A(2,0),B(0,-1)和C(4,5)三点。
的图象过A(2,0),B(0,-1)和C(4,5)三点。 轴的另一个交点为D,求点D的坐标;
轴的另一个交点为D,求点D的坐标;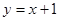 ,并写出当
,并写出当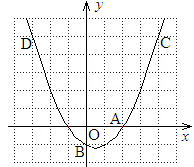
 中,抛物线
中,抛物线 经过点
经过点 (0,
(0, ),
), (3,4).
(3,4). ,点
,点 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在 (包含
(包含 与图象
与图象 的取值范围.
的取值范围.
 (a≠0)的图象经过点A,点B.
(a≠0)的图象经过点A,点B. (x>0)的图象与二次函数
(x>0)的图象与二次函数 ,
, 落在两个相邻的正整数之间,请你直接写出这两个相邻的正整数;
落在两个相邻的正整数之间,请你直接写出这两个相邻的正整数; (x>0,k>0)的图象与二次函数
(x>0,k>0)的图象与二次函数 ,且
,且 ,试求实数k的取值范围.
,试求实数k的取值范围.
 的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.
的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线. ,求点M的坐标.
,求点M的坐标.

 的一元二次方程
的一元二次方程 有实数根,
有实数根, 为正整数.
为正整数. 的图象向下平移2个单位,求平移后的函数图象的解析式;
的图象向下平移2个单位,求平移后的函数图象的解析式; 轴左侧的部分沿
轴左侧的部分沿 与图象G有3个公共点时,请你直接写出
与图象G有3个公共点时,请你直接写出 的取值范围.
的取值范围.