Question

如图，已知二次函数（a≠0）的图象经过点A，点B．
（1）求二次函数的表达式；
（2）若反比例函数（x＞0）的图象与二次函数（a≠0）的图象在第一象限内交于点，落在两个相邻的正整数之间，请你直接写出这两个相邻的正整数；
（3）若反比例函数（x＞0，k＞0）的图象与二次函数（a≠0）的图象在第一象限内交于点，且，试求实数k的取值范围．

Answer 1

（1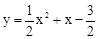）；（2）1与2；（3）5 < k < 18.

解析试题分析：（1）由图可知：点A、点B的坐标分别为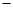（3,0），（1,0），把（1，0），和（-3，0）分别代入函数关系式得到方程组，解方程组，得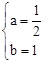，所以抛物线解析式为.
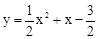（2）观察函数的图象可以得到相邻的两个正整数为1和2.
（3）由函数图象或函数性质可知两个函数的增减性.所以当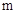=2时，反比例函数图象在二次函数的图象上方，得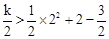并由此解得k的取值范围；当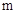=3时，二次函数的图象在反比例函数图象上方的，得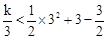，并由此也可以求得k的取值范围，从而得到k完整的取值范围．
试题解析：（1）由图可知：点A、点B的坐标分别为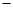（3,0），（1,0），
且在抛物线上，
∴，解得：  .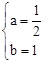
∴二次函数的表达式为.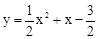
（2）正确的画出二次函数和反比例函数在第一象限内的图象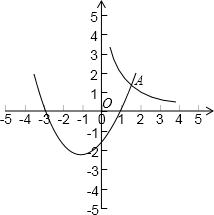

由图象可知，这两个相邻的正整数为1与2．
（3）由题意可得：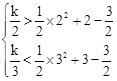
 ，解得：5 < k < 18.
∴实数k的取值范围为5 < k < 18.
考点：二次函数综合题．