题目内容
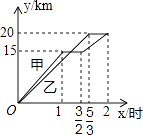
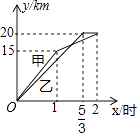
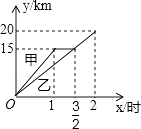
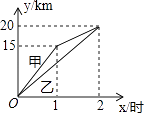
【题目】如图,一次函数![]() (
(![]() )与反比例函数
)与反比例函数![]() (
(![]() )的图象交于点
)的图象交于点![]() ,
,![]() .
.
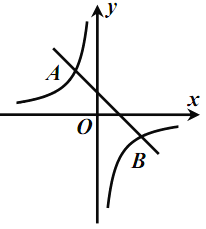
(1)求这两个函数的表达式;
(2)在![]() 轴上是否存在点
轴上是否存在点![]()
![]() ,使
,使![]() 为等腰三角形?若存在,求
为等腰三角形?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1) 反比例函数的解析式为y=-![]() .一次函数的解析式为y=-x+1.(2) n=-1+
.一次函数的解析式为y=-x+1.(2) n=-1+![]() 或2+
或2+![]() .
.
【解析】
试题分析:(1)利用待定系数法即可解决问题;
(2)分三种情形讨论①当PA=PB时,可得(n+1)2+4=(n-2)2+1.②当AP=AB时,可得22+(n+1)2=(3![]() )2.③当BP=BA时,可得12+(n-2)2=(3
)2.③当BP=BA时,可得12+(n-2)2=(3![]() )2.分别解方程即可解决问题;
)2.分别解方程即可解决问题;
试题解析:(1)把A(-1,2)代入y=![]() ,得到k2=-2,
,得到k2=-2,
∴反比例函数的解析式为y=-![]() .
.
∵B(m,-1)在y=-![]() 上,
上,
∴m=2,
由题意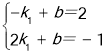 ,解得
,解得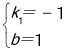 ,
,
∴一次函数的解析式为y=-x+1.
(2)∵A(-1,2),B(2,-1),
∴AB=3![]() ,
,
①当PA=PB时,(n+1)2+4=(n-2)2+1,
∴n=0,
∵n>0,
∴n=0不合题意舍弃.
②当AP=AB时,22+(n+1)2=(3![]() )2,
)2,
∵n>0,
∴n=-1+![]() .
.
③当BP=BA时,12+(n-2)2=(3![]() )2,
)2,
∵n>0,
∴n=2+![]() .
.
综上所述,n=-1+![]() 或2+
或2+![]() .
.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
【题目】下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 ![]() 与方差s2:
与方差s2:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2(cm2) | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲
B.乙
C.丙
D.丁