题目内容
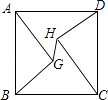
【题目】如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.
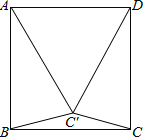
【答案】△DCC′,△DC′A,△C′AB,△C′BC,理由见解析.
【解析】
试题利用旋转的性质以及正方形的性质进而得出等腰三角形,再利用全等三角形的判定与性质判断得出.
试题解析:图中的等腰三角形有:△DCC′,△DC′A,△C′AB,△C′BC,理由如下:
∵四边形ABCD是正方形,∴AB=AD=DC,∠BAD=∠ADC=90°.∴DC=DC′=DA.
∴△DCC′,△DC′A为等腰三角形.
∵∠C′DC=30°,∠ADC=90°,∴∠ADC′=60°.∴△AC′D为等边三角形.
∵∠C′AB=90°-60°=30°,∴∠CDC′=∠C′AB.
在△DCC′和△AC′B中CD=BA,∠CDC′=∠C′AB,C′D=C′A,
∴△DCC′≌△AC′B(SAS).∴CC′=C′B,∴△BCC′为等腰三角形.

练习册系列答案
相关题目