题目内容
【题目】如图，直线y=
x+2交x轴于点A，交y轴于点B，点P（x，y）是线段AB上一动点（与A，B不重合），△PAO的面积为S，求S与x的函数关系式，并写出自变量的取值范围.
【答案】
【解析】
试题首先求得点A的坐标，然后根据点P在直线y=
x+2上，从而表示出点P的坐标为（x，x+2），然后利用三角形的面积计算方法表示出三角形的面积即可．
解：∵令y=x+2=0，解得：x=-4，
∴点A的坐标为（-4，0），
∵令x=0，得y=2，
∴点B的坐标为（0，2），
∴OA=4，OB=2，
∵点P（x，y）是线段AB上一动点（与A，B不重合），
∴点P的坐标可表示为（x，x+2），
如右图，作PC⊥AO于点C，
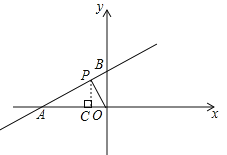
∵点P（x，x+2）在第二象限，
∴x+2＞0
∴PC=x+2
∴S=AOPC
=×4×（x+2）
=x+4．
∴S与x的函数关系式为S=x+4（-4＜x＜0）．
练习册系列答案
相关题目
【题目】某商店用 500 元购进 A、B 两种铅笔盒共 50 个，这两种铅笔盒的进价、标价如下表所示．
类型 价格 | A 型 | B 型 |
进价（元/个） | 8 | 13 |
标价（元/个） | 12 | 20 |
（1）这两种笔记本各购进多少个？
（2）若 A 型笔记本按标价的 9 折出售，B 型笔记本按标价的 8 折出售，那么这批笔记本 全部售出后，商店共获利多少元？
