Question

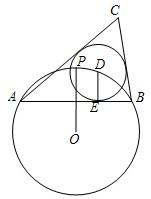如图，⊙O的半径为1，点P是⊙O上一点，弦AB垂直平分线段OP，点D是

APB

上任一点（与端点A、B不重合），DE⊥AB于点E，以点D为圆心、DE长为半径作⊙D，分别过点A、B作⊙D的切线，两条切线相交于点C．
（1）求弦AB的长；
（2）判断∠ACB是否为定值？若是，求出∠ACB的大小；否则，请说明理由；
（3）记△ABC的面积为S，若

S

DE2

=4

3

，求△ABC的周长．

Answer 1

分析：（1）连接OA，OP与AB的交点为F，则△OAF为直角三角形，且OA=1，OF=

1

2

，借助勾股定理可求得AF的长；
（2）要判断∠ACB是否为定值，只需判定∠CAB+∠ABC的值是否是定值，由于⊙D是△ABC的内切圆，所以AD和BD分别为∠CAB和∠ABC的角平分线，因此只要∠DAE+∠DBA是定值，那么CAB+∠ABC就是定值，而∠DAE+∠DBA等于弧AB所对的圆周角，这个值等于∠AOB值的一半；
（3）由题可知S=S_△ABD+S_△ACD+S_△BCD=

1

2

DE（AB+AC+BC），又因为

S

DE2

=4

3

，所以AB+AC+BC=8

3

DE，由于DH=DG=DE，所以在Rt△CDH中，CH=

3

DH=

3

DE，同理可得CG=

3

DE，又由于AG=AE，BE=BH，所以AB+AC+BC=CG+CH+AG+AB+BH=2

3

DE+2

3

，可得8

3

DE=2

3

DE+2

3

，解得：DE=

1

3

，代入AB+AC+BC=8

3

DE，即可求得周长为

8 3

3

．

解答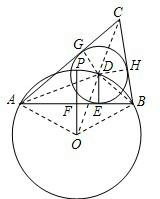：解：（1）连接OA，取OP与AB的交点为F，则有OA=1．
∵弦AB垂直平分线段OP，
∴OF=

1

2

OP=

1

2

，AF=BF，
在Rt△OAF中，
∵AF=

OA2-OF2

=

12-( 1 2 )2

=

3

2

，
∴AB=2AF=

3

．

（2）∠ACB是定值．
理由：连接AD、BD，
由（1），OF=

1

2

，AF=

3

2

，
∴tan∠AOP=

AF

OF

=

3

，
∴∠AOP=60°，
∴∠AOB=120°，
∵点D为△ABC的内心，
∴∠CAB=2∠DAE，∠CBA=2∠DBA，
∵∠DAE+∠DBA=

1

2

∠AOD+

1

2

∠DOB=

1

2

∠AOB=60°，
∴∠CAB+∠CBA=120°，
∴∠ACB=60°．

（3）记△ABC的周长为l，取AC，BC与⊙D的切点分别为G，H，连接OD．
连接DG，DC，DH，则有DG=DH=DE，DG⊥AC，DH⊥BC，
∴S=S_△ABD+S_△ACD+S_△BCD
=

1

2

AB•DE+

1

2

BC•DH+

1

2

AC•DG=

1

2

（AB+BC+AC）•DE=

1

2

l•DE，
∵

S

DE2

=4

3

，
∴

1 2 l•DE

DE2

=4

3

，
∴l=8

3

DE，
∵CG，CH是⊙D的切线，
∴∠GCD=

1

2

∠ACB=30°，
∴在Rt△CGD中，CG=

DG

tan30°

=

DE

3 3

=

3

DE，
∴CH=CG=

3

DE，
又由切线长定理可知AG=AE，BH=BE，
∴l=AB+BC+AC=2

3

+2

3

DE=8

3

DE，
解得DE=

1

3

，
∴△ABC的周长为

8 3

3

．

点评：本题巧妙将垂径定理、勾股定理、内切圆、切线长定理、三角形面积等知识综合在一起，需要考生从前往后按顺序解题，前面问题为后面问题的解决提供思路，是一道难度较大的综合题．